Теорема деления (теорема о делении с остатком)

Основные понятия и теоремы.

Предмет теории чисел – целые числа и их свойства.

Множество целых чисел обозначается символом Z, символом Z₊ обозначается множество целых положительных чисел, символом N– множество натуральных чисел. Латинскими малыми буквами здесь и далее будем обозначать целые числа.

Заметим, что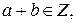

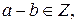
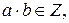
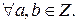
То есть как сумма, так и произведение целых чисел также являются целыми числами. Частное двух целых чисел не всегда является целым числом.

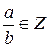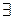
Если , (b≠0) 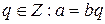, 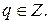Тогда говорят, что а делится на b, или b делит а, и пишут b\a. Тогда а называем кратным числа b, а b – делителем числа а.

Справедливы следующие

Теоремы:

(1) m\a, b\m b\a.

Доказательство:

m\a a=ma₁;

b\m m=bm₁ a=bm₁a₁. Обозначив b₁=a₁m₁, получим a=bb₁, причем 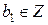b\a.

□

(2) Если в равенстве вида k+l+…+n=p+q+…+s относительно всех членов кроме одного известно, что они кратны b, то и один оставшийся член тоже кратен b.

Доказательство:

Не нарушая общности, предположим, что таким членом (относительно кратности которого числу b ничего не известно) является k.

Тогда 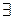l₁, …, n₁, p₁, q₁, …, s₁: l=bl₁,…, n=bn₁, p=bp₁, q=bq₁, …, s=bs₁.

Тогда k=p+q+…+s–l–…–n=bp₁+bq₁+…+bs₁–bl₁–…–bn₁=b(p₁+q₁+…+s₁–l₁–…–n₁)

Обозначим k₁= p₁+q₁+…+s₁–l₁–…–n₁. Очевидно, k₁ – целое число, причем k=bk₁ Тогда, по определению делимости, b\k.

□

Кроме того, очевидны следующие свойства:

1) 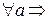a\0, 1\a, a\a.

2) a\b, b\a a=±b.

3) a\b, a\c 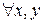a\(bx+cy).

(Доказательство св-ва 3: b=ab₁, c=ac₁ bx+cy=ab₁x+ac₁y=a(b₁x+c₁y))

Теорема деления (теорема о делении с остатком)

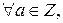
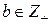
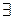единственная пара чисел 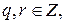0 ≤ r < b: a=bq+r *

Доказательство:

Возьмем q: bq≤a, b(q+1)>a. Такое целое q, очевидно, существует r=a–bq является целым положительным числом как разность двух целых чисел, первое из которых больше второго. Причем выполняется 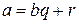. Построением такого r доказано существование разложения (*).

Теперь докажем единственность разложения (*): предположим, что кроме построенного выше, имеется еще одно разложение числа a:

a=bq₁+r₁, 0≤r₁<b.

Вычтем полученное равенство из равенства (*) почленно. Получим

0=b(q–q₁)+(r–r₁). **

Поскольку b\0, b\b(q–q₁), то по теореме 2, b\(r–r₁).

С другой стороны, 0≤r<b, 0≤r₁<b |r–r₁|<b. Отсюда и из того, что b\(r–r₁), следует, что r–r₁=0, и тогда r=r₁. Подставляя полученное равенство в (**), получаем 0=b(q–q₁).

Но по условию теоремы, b≠0 , тогда q–q₁=0 q=q₁.

Таким образом, оба построенных разложения числа a совпадают, а значит разложение (*) единственно.

□

В разложении (*) число q называются неполным частным, r – остатком от деления a на b.