Бинарный алгоритм Евклида
Этот вариант создан специально для реализации на ЭВМ. В нем учитывается, что операция деления на число 2 или на любую степень двойки является весьма быстрой и простой операцией (в двоичной системе счисления операция деления на 2 есть всего лишь битовый сдвиг вправо).
Учтем, что (2k∙a,2s∙b)=2min(k,s)(a,b).
Алгоритм:
Вход: a, b>0.
1. Представим a и b в виде: 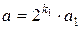 ;
; 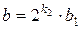 , где a1, b1 – нечетные числа.
, где a1, b1 – нечетные числа.
k:=min(k1,k2).
2. Если a1>b1  Шаг 4
Шаг 4
a1< b1  Шаг 3
Шаг 3
a1= b1  Шаг 6
Шаг 6
3. Меняем местами a1 и b1.
4. c:=a1–b1=2s∙c1 (c1 - нечетное число)
(Заметим, что с обязательно будет четным, а значит 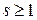 )
)
5. a1:= b1 , b1:=c1 . Возвращаемся на Шаг 1.
6. Выход: (a,b)=2k∙a1 .
Пример
a=603, b=108
| a1 | |||
| b1 | |||
| c1 | – |
1. a1=603, k1=0; b=108=4∙27=22∙27  k2=2, b1=27, k=0
k2=2, b1=27, k=0
2. a1=603> b1=27  Ш4
Ш4
4. c=603-27=56=64∙9, c1=9
5. a1=27; b1=9  Ш1
Ш1
1. a1=27; b1=9
2. a1> b1  Ш4
Ш4
4. c=a1–b1=18=2∙9, c1=9
5. a1=9, b1=9
1. a1=9, b1=9, k=0
2. a1= b1  Ш6
Ш6
6. (a,b) = 2º∙9=9
Для НОД справедливы следующие свойства:
1) (am,bm)=m(a,b) 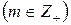
Доказательство:
Доказательство строится, умножая почленно соотношения алгоритма Евклида на m.
2) d – общий делитель чисел a и b 
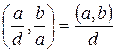
(в частности, 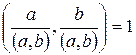 ).
).
Доказательство:
Учитывая, что 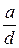 и
и 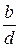 – целые числа, из свойства НОД №1 получаем соотношение
– целые числа, из свойства НОД №1 получаем соотношение 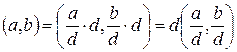

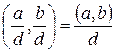 , что и требовалось.
, что и требовалось.
□
3) (a,b)=1  (ac,b)=(c,b)
(ac,b)=(c,b)
Доказательство:
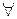 a, b, c выполняется (ac,b)\ac, (ac,b)\b
a, b, c выполняется (ac,b)\ac, (ac,b)\b  (ac,b)\bc
(ac,b)\bc  (ac,b)\(ac,bc).
(ac,b)\(ac,bc).
По условию теоремы, в силу взаимной простоты a и b  (ac,bc)=c, то есть получили (ac,b)\с.
(ac,bc)=c, то есть получили (ac,b)\с.
Но (ac,b)\b  (ac,b)\(c,b).
(ac,b)\(c,b).
С другой стороны, (c,b)\ac, (c,b)\b.  (c,b)\(ac,b).
(c,b)\(ac,b).
Таким образом, числа (ac,b) и (c,b). взаимно делят друг друга  (ac,b)=(c,b).
(ac,b)=(c,b).
□
4) (a,b)=1, b\ac  b\c.
b\c.
Доказательство:
Из теоремы №1 о НОД в силу b\ac,  (ac,b)=b.
(ac,b)=b.
из свойства НОД № 3  b=(c,b)и тогда из теоремы №1 о НОД b\c.
b=(c,b)и тогда из теоремы №1 о НОД b\c.
□
5) Если (ai, bj)=1 для 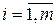 ,
, 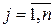
 (
( 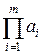 ,
, 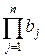 )=1.
)=1.
Доказательство:
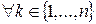 имеем (
имеем ( 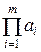 ,
, 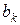 ) = (
) = ( 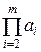 ,
, 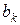 ) = (
) = ( 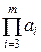 ,
, 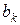 ) = … =
) = … = 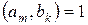 .
.
Аналогично, используя полученное соотношение,
( 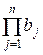 ,
, 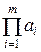 ) = (
) = ( 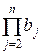 ,
, 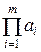 ) = … = (
) = … = ( 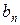 ,
, 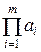 ) = 1.
) = 1.
□
Дата добавления: 2018-11-26; просмотров: 1189;











