Наибольший общий делитель.

Далее будем рассматривать лишь положительные делители чисел.

Общим делителем чисел a₁, a₂,…,a_n называется число d: d\a_i .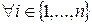

Наибольший из всех общих делителей чисел a₁, a₂,…,a_n называется их наибольшим общим делителем (НОД) и обозначается НОД(a₁, a₂,…,a_n) или (a₁, a₂,…,a_n).

Если (a₁, a₂,…,a_n)=1, то числа a₁, a₂,…,a_n называются взаимно простыми.

Если (a_i,a_j)=1 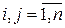, i≠j , то числа a₁, a₂,…,a_n называются попарно простыми.

Утверждение

Если числа a₁, a₂,…,a_n – попарно простые, то они взаимно простые. (Очевидно.)

Теорема 1

Если b\a совокупность общих делителей a и b совпадает с совокупностью делителей b. В частности, (a,b)=b.

Доказательство:

b\a a=ba₁, тогда 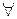d: d\b справедливо d\a (т.е. любой делитель b является также делителем a).

Если l\a, но l не делит b, то l не является общим делителем a и b.

То есть совокупность общих делителей a и b совпадает с совокупностью делителей b. А поскольку наибольший делитель b есть b, и b\a , то (a,b)=b.

□

Теорема 2

Если a=bq+c, то совокупность общих делителей a и b совпадает с совокупностью общих делителей b и c.

В частности, (a,b)=(b,c)

Доказательство:

Пусть m\a, m\b m\c (в силу a=bq+c и теоремы 2 п.1), а значит m – общий делитель b и c.

Пусть l\b, l\c l\a (в силу a=bq+c и теоремы 2 п.1), а значит l - общий делитель a и b.

Получили совпадение совокупности общих делителей a и b и общих делителей b и c.

Пусть теперь d=(a,b) d\a, d\b, а значит, по доказанному выше, d\c. В силу совпадения совокупностей общих делителей и того, что d – наименьший изо всех делителей a и b, не может существовать d₁: d₁>d, d₁\b, d₁\c. Поэтому d=(b,c) (a,b)= (b,c).

□