Уравнение состояния реального газа.
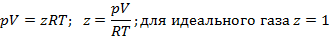

Рисунок 163. Зависимость коэффициента сжимаемости от давления для различных веществ.
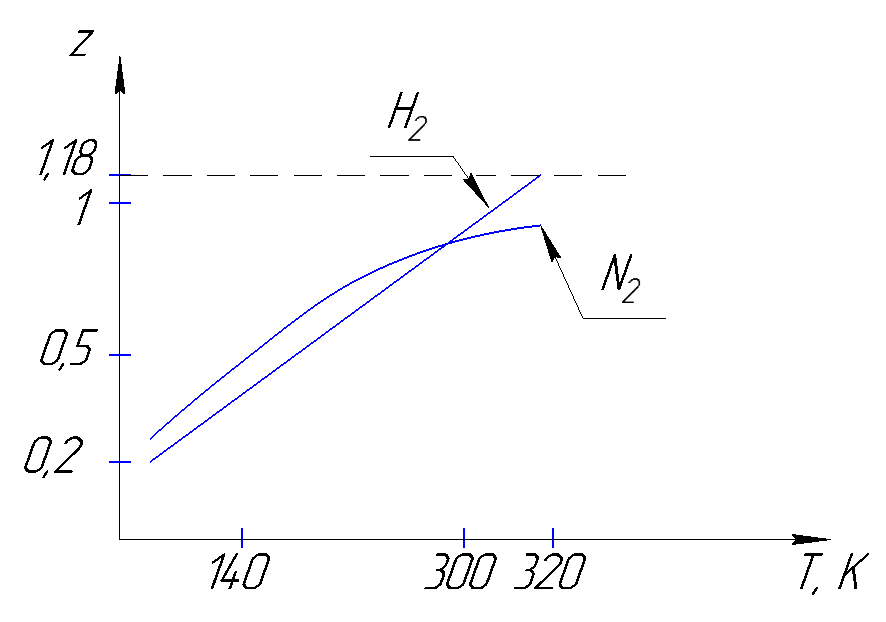
Рисунок 164. Зависимость коэффициента сжимаемости от температуры для различных веществ.
Уравнение Ван-дер-Ваальса

a – учитывает увеличение давления вследствие взаимодействия молекул газа;
b – учитывает собственный объем молекул.
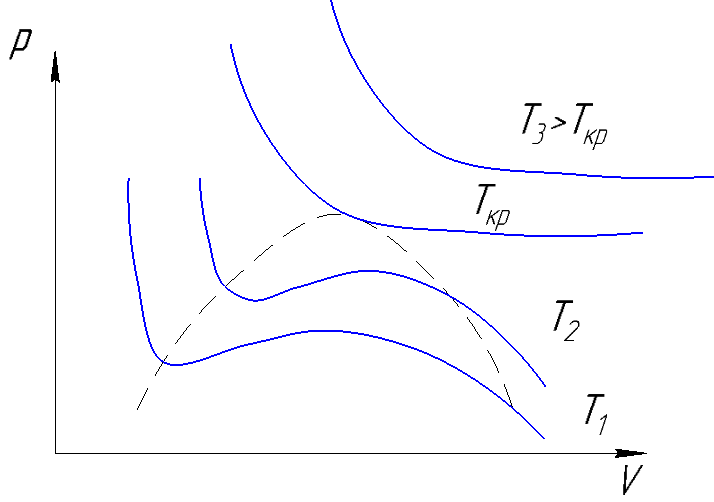
Рисунок 165. Уравнение Ван-дер-Ваальса в PV координатах.
Чаще всего уравнение Ван-дер-Ваальса используется не в исходном виде, а через безразмерные T, p, V, которые выражаются через критические параметры:
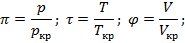
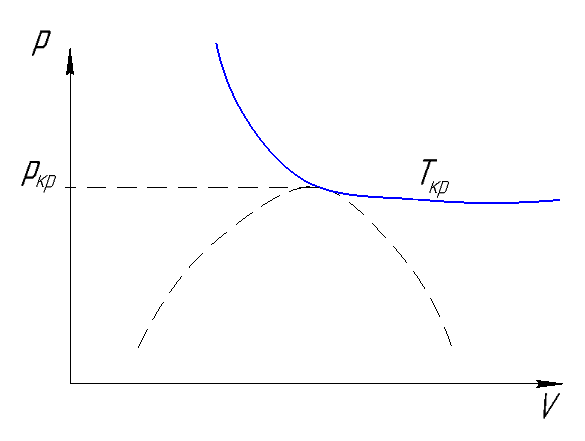
Рисунок 166. Критическая изотерма в PV.
Критическая точка характеризуется тем, что первая и вторая производные параметров состояния обращаются в нуль:
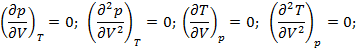
Также обращается в ноль вторая производная p и T по энтропии:
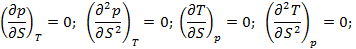
Воспользуемся выражением первой и второй производной в критической точке для определения связи a и b и параметров критической точки
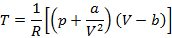

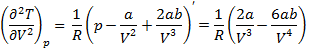
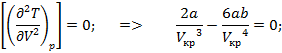

Приравняем к нулю первую производную:
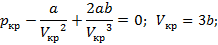

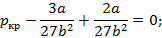
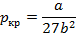
Для определения критической температуры воспользуемся обращением в нуль:

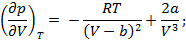
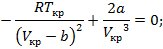

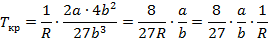
Переписываем уравнение Ван-дер-Ваальса через критические параметры и безразмерные величины:

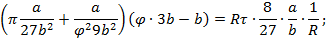

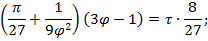
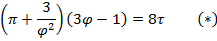
Уравнение Ван-дер-Ваальса в безразмерных параметрах справедливо для любого вещества.
Найдем из уравнения Ван-дер-Ваальса уравнение кривой инверсии:
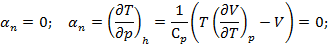
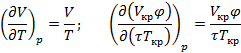

Из 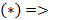 Вводим функцию:
Вводим функцию:

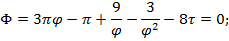
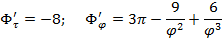
Лекция №26
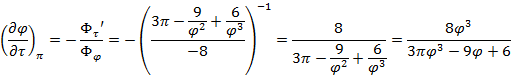
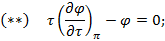
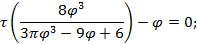
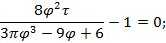
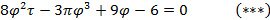
Используя  и
и 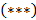 найдем уравнение линии инверсии в координатах
найдем уравнение линии инверсии в координатах 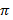 и
и 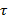 :
:
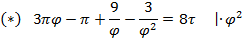
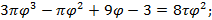
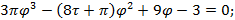
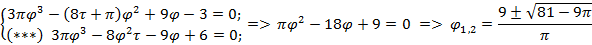

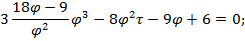
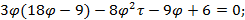
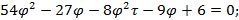
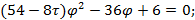
. . . . . .
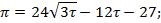
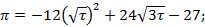 -уравнение линии инверсии
-уравнение линии инверсии
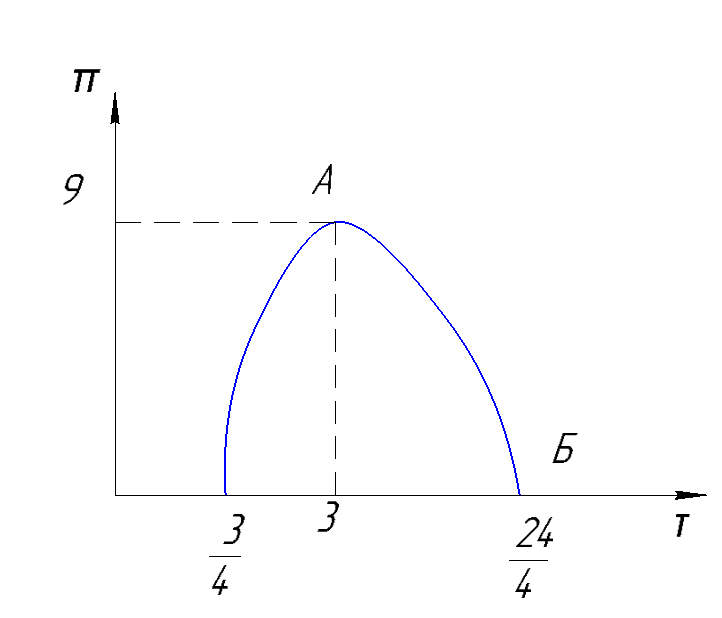
Рисунок 167. Кривая инверсии.
т.А: 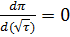
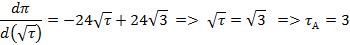

т.Б: 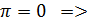
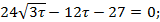
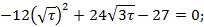


Дата добавления: 2016-06-22; просмотров: 1991;











