Теплопроводность твердых тел.
При переносе теплоты за счет теплопроводности в твердом теле существует три способа:
1. за счет движения электронов, что характерно для проводников;
2. за счет колебаний решетки или энергии фотонов (Для всех твердых тел);
3. за счет движения молекул, что характерно для органических твердых тел;
Из теории переноса коэффициент теплопроводности можно определить по следующей формуле:
 [
[ 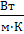 ]
]
Коэффициент теплопроводности –физическая величина ,равная количеству теплоты, передаваемого в единицу времени через единичную площадь сечения тела при единичном градиенте температуры, в направлении перпендикулярно единичной поверхности.
Лекция №24 05.12.2014
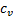 -удельная теплоемкость V=const;
-удельная теплоемкость V=const;
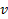 -скорость движения частиц;
-скорость движения частиц;
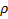 -плотоность вещества;
-плотоность вещества;
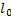 - средняя длина пробега частиц;
- средняя длина пробега частиц;
Для металлов энергия переносится за счет движения электронов и фотонов, причем действие электронной и фотонной части теплопроводности различаются в зависимости от температурного уровня. Для электропров. при Т>80˚К основной вклад дают электроны, длина 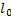 обратно пропорциональна абсолютной температуре. T˂80˚К (жидкий
обратно пропорциональна абсолютной температуре. T˂80˚К (жидкий 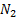 ) вклад электронов становится меньше и λ~
) вклад электронов становится меньше и λ~ 
В данном случае λ↑ при Т↓ и достигает максимального значения, когда 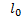 становится соизмеримо с размером образца.
становится соизмеримо с размером образца.
Для сплавов или нечистых металлов эти соотношения не пригодны ,поскольку для веществ с неупорядоченной структурой имеет место рассеяние энергии Е ~Т.
Поэтому достижение эфф. максимума теплопроводности у сплавов и нечистых металлов нет.
| Материал Т,˚К | Алюминиевый сплав | Нержавеющая сталь | Углеродистая сталь | Чистая медь |
| 0,8 | ||||
| 0,1 |
Теплоемкость твердого тела.
Обычно рассматривается изохорная 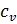
Для одноатомного кристаллического твердого тела обычно используют формулу Дебая.
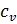 =3R(
=3R( 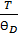 )3f(
)3f( 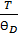 )
)
R-газовая const
 -температура Дебая;
-температура Дебая;
f( 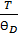 )-функция Дебая;
)-функция Дебая;
| вещество | Al | Cu | α-Fe | γ-Fe | Ne | Ag | Бел Sn | Сер Sn | T |
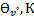
|
Зависимость от безразмерной температуры Дебая ( 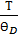 ) для твердых тел имеет следующий вид:
) для твердых тел имеет следующий вид:

Рисунок 157. Зависимость безразмерной теплоёмкости от безразмерной температуры.
При Т>3Ɵ 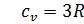 -Закон Дюлонга-Пти
-Закон Дюлонга-Пти
При Т˂ 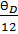 =>
=> 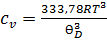
Дебай рассматривал свою теорию теплоемкости без учета движения электронов –только кристаллическую решетку металла. Электроны вносят свой вклад в суммарную теплоемкость в зависимости от Т:

| металл | Al | Cu | Fe | Ni | Ag | Ti |
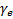 ,мДж/кг·К2 ,мДж/кг·К2
| 50,4 | 11,0 | 89,9 | 5,65 | 74,1 |
Вклад электронной составляющей в теплоемкость обычно не превышает нескольких процентов.
cv,Ʃ=cv +cv,e
Коэффициент теплового расширения твердых тел.
∆l= 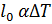
Α [ 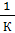 ] , α=
] , α=  (
(  )
)
Зависимость коэффициента линейного расширения от Т имеет близкий вид к теплоемкости и описывается примерно теми же выражениями в области температур
T< 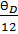 , где α~T3
, где α~T3

Рисунок 158. Зависимость коэффициента линейного теплового расширения от температуры.
Удельное электрическое сопротивление.
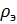 [Ом·м]
[Ом·м]
С понижением температуры у металлов величина электр. сопротивления падает. Механизм переноса электрического заряда в металле тождественно переносу теплоты. Обе эти величины связаны законом Видемана-Франца:
λ 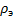 =BT
=BT
B=24,45 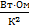
При низких температурах вблизи темп. жидкого азота наблюдается явление сверхпроводимости.
Свойство криогенных жидкостей.
1. Плотность.
Будем рассматривать только насыщенную жидкость.
С повышением ρ плотность равновесной жидкости падает, а плотность равновесного пара растет.
Например, жидкий N2 T=125 К; ρm=431 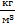 ;
;
T=78 К; ρm=804,3 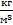 ;
;
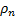 =4,98
=4,98
Чем ↑ρ, тем ниже критическая точка.
Равновесная плотность жидкости и газа связаны между собой уравнением прямой линии
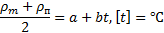
| Вещество | He | Ne | H2 | N2 | O2 |
| a | -0,4 | -1,15 | -0,063 | 0,0229 | 0,16 |
| b | -0,017 | -0,0071 | 0,000394 | -0,00196 | -0,0022 |
Плотность смеси определяется по специальной формуле:
Ρсм= 
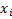 -массовая доля компонента смеси;
-массовая доля компонента смеси;
Коэффициент объемного расширения для сжиженных газов.
β= 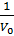
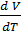 [
[  ]; β=3α
]; β=3α
| вещество | Ar | N2 | O2 | H2 |
| β | 0,00545 | 0,00588 | 0,00385 | 0,0126 |
Вязкость насыщенных жидкостей.
С падением Т вязкость ↑ за исключением He, который при Т↓ 2,2К становится сверхтекучим.
ɱн.жид-ти=A·ec/T
A, c-const для рабочего тела
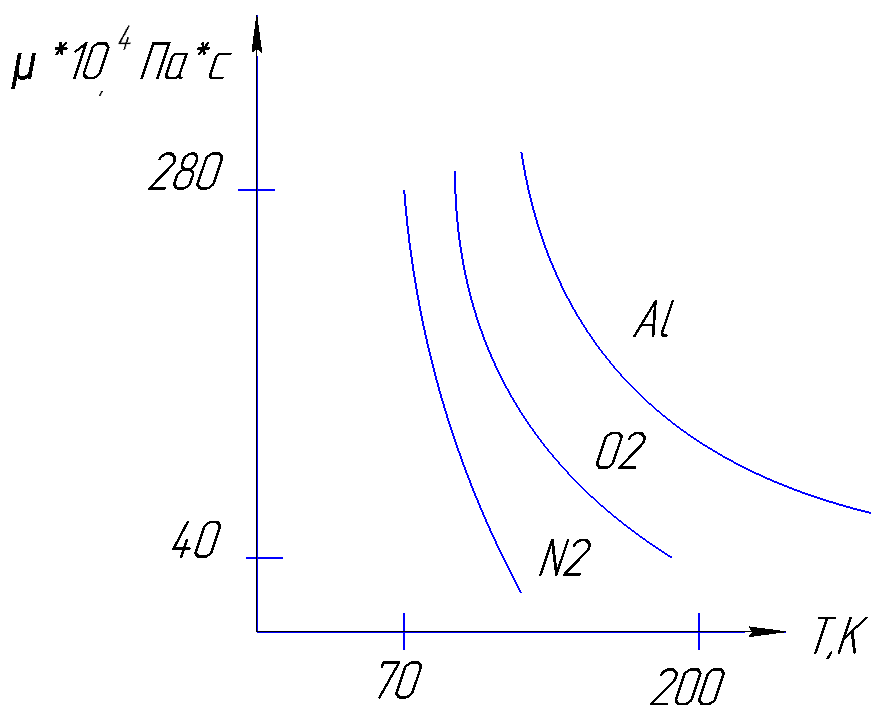
Рисунок 159. Зависимость динамической вязкости от температуры.
Вязкость жидкой смеси.
ln ɱсм=n1·ln ɱ1+ n2·ln ɱ2+…+ nk·ln ɱk
ni [ 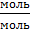 ]- молярная доля компонента смеси.
]- молярная доля компонента смеси.
Теплопроводность насыщенной жидкости.
С понижением Т теплопроводность ↑ для всех веществ кроме Н2 и Не.
У Н2 понижается ,а у Не вначале понижается , а затем увеличивается при переходе в сверхтекучее состояние, достигает максимума при Т=1,8 К, а затем падает.
Для большинства жидкостей величину теплопроводности можно определить по формуле Вебера:
λ=1,28· 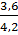 ρсР (
ρсР ( 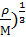
ρ-плотность ; СР- изобарная теплоемкость; М –молекулярная масса жидкости;
Теплоемкость криогенных жидкостей.
Для всех веществ кроме Не с понижением температуры теплоемкость ↓
У Не вблизи Т перехода в сверхтекучее состояние наблюдается скачок теплоемкости λперех

Рисунок 160. Лямбда точка гелия.
Коэффициент поверхностного натяжения криогенных жидкостей.
Коэффициент увеличивается с понижением Т
Ϭ [  ]
]
N2: Ϭ|120K=0,65·10-5 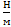 ; Ϭ|80K=8,28·10-5
; Ϭ|80K=8,28·10-5 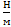
H2: Ϭ|23K=1,69·10-5 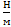 ; Ϭ|16K=2,95·10-5
; Ϭ|16K=2,95·10-5 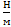
O2: Ϭ|90K=13,2·10-5 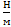 ; Ϭ|70K=18,3·10-5
; Ϭ|70K=18,3·10-5 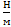
He: Ϭ|4,2K=0,09·10-5 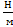 ; Ϭ|3K=0,22·10-5
; Ϭ|3K=0,22·10-5 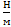
Лекция №25 08.12.2014
Коэффициент преломления криогенных жидкостей.
| жидк | N2 | H2 | He | O2 | H2O |
| n | 1,205 | 1,09 | 1,02 | 1,221 | 1,332 |
Диэлектрическая постоянная жидкости.
| жидк | He | H2 | N2 | Ar | CH4 |
| ε | 1,05 | 1,24 | 1,45 | 1,52 | 1,7 |
Ослабление электростатического поля по отношению к вакууму.
Свойства газов.
1. Вязкость.
Достаточно хорошо описывается формулой Сазерленда:
η=η0  (
( 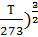
η0-вязкость при 1 атм и 2730К
| газ | N2 | Ar | H2 | воздух | He | Ne | O2 |
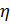 0·106 Па·с 0·106 Па·с
| 84,2 | ||||||
| C |
Зависимость от давления достаточно слабая; с увеличением давления дин. вязкость увеличивается, но не более , чем на 5%в диапазоне до 60 атм.
Отклонение от формулы Сазерленда ,которая выведена для идеального газа тем больше, чем реальный газ отличается от идеального.
Вязкость смеси определяется по формуле кинетической вязкости в зависимости от дольной моли:
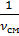 =
= 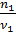 +
+  +… +
+… + 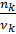
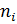 [
[ 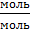 ]
]
ɱ=ρν
2. Теплопроводность для идеального газа также определяется по формуле Сазерленда:
λ=λ0 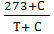 (
( 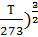
с-аналогично; λ0-коэффициент теплопроводности для 1 атм и 273°К
| газ | N2 | Ar | H2 | воздух | He | Ne | O2 |
λ, 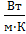
| 0,0238 | 0,0173 | 0,1665 | 0,0244 | 0,144 | 0,0455 | 0,0243 |
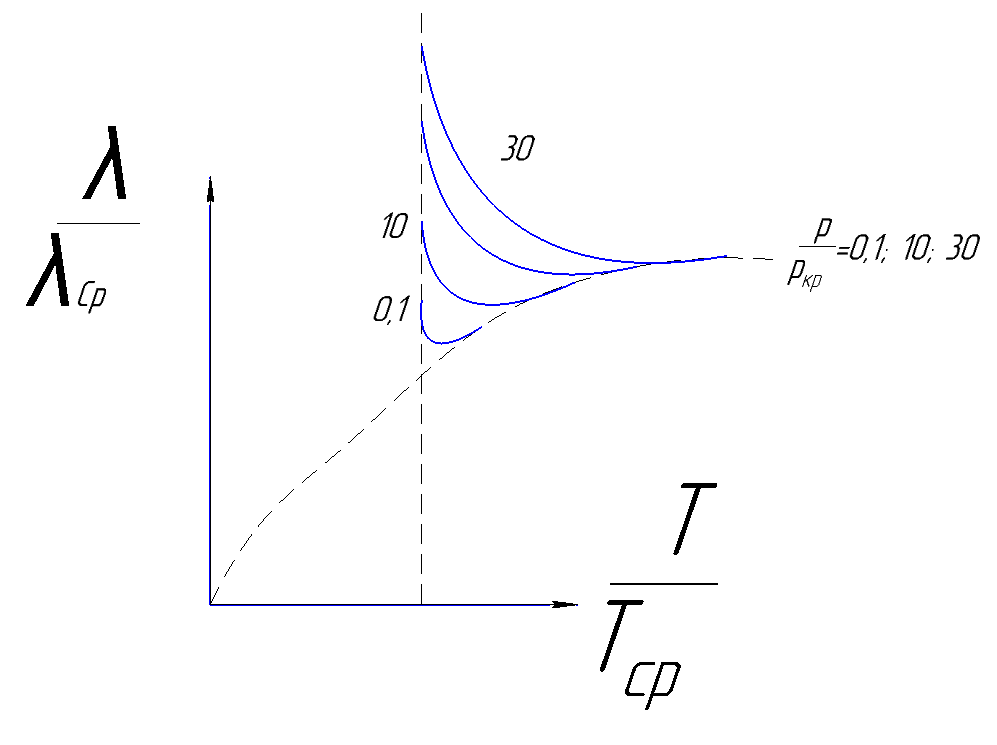
Рисунок 161. Зависимость относительной теплопроводности от относительной температуры.
Теплопроводность смеси для всех газов, кроме Н2, Не
λст=n1λ1+ n2λ2+…+nkλk
H2,He: λcм=a∑niλi+(1-a) 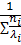
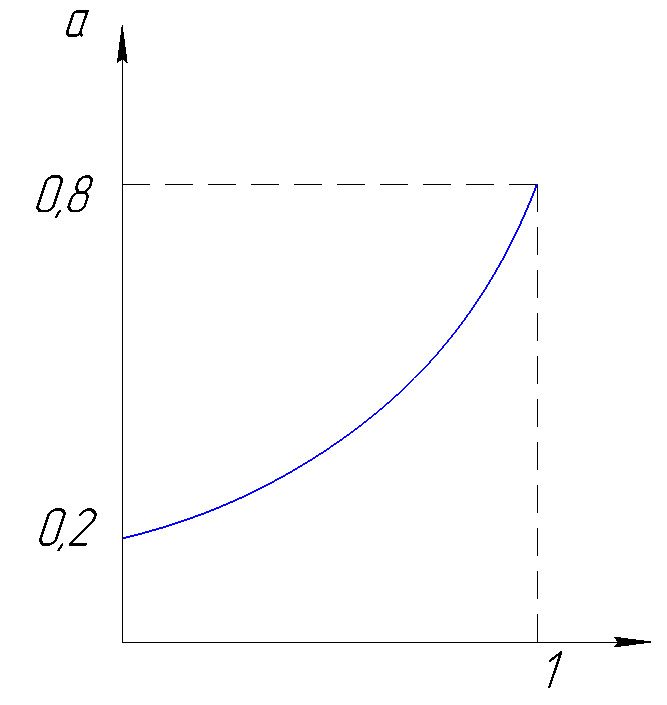
Рисунок 162. Зависимость коэффициента а.
Теплоёмкость газа
Для идеального газа справедлива формула Майера:
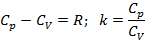
Теплоёмкость реального газа резко зависит от T и p и не описывается никакими аналитическими зависимостями.
Дата добавления: 2016-06-22; просмотров: 4740;











