Критерии оценки направления самопроизвольного протекания процессов
| Характеристика системы | Критерий оценки | Условие равновесия | Условие протекания самопроизвольного процесса |
| Изолированная система | Энтропия S | ΔS = 0, S = Smax | ΔS > 0 |
| Неизолированная система, р,Т = const | Изобарно-изотермический потенциал G | ΔG = 0, G = Gmin | ΔG < 0 |
| Неизолированная система, V, Т = const | Изохорно-изотермический потенциал F | ΔF = 0, F = Fmin | ΔF < 0 |
Раздел II. растворы и гетерогенные равновесия
Основные понятия и определения
Вещества, образующие термодинамическую систему, могут находиться в различных агрегатных состояниях: газообразном, жидком, твердом.
Термодинамическая система, внутри которой нет поверхностей раздела, отделяющих различные либо по физическому строению, либо по химическим свойствам части системы, называется гомогенной.
Термодинамическая система, состоящая из различных по физическим или химическим свойствам частей, отделенных друг от друга поверхностями раздела, называется гетерогенной.
Любая гетерогенная система состоит из нескольких фаз.
Фаза– это часть гетерогенной системы, ограниченная поверхностью раздела и характеризующаяся одинаковыми физическими и химическими свойствами во всех точках.
Различают однофазные, двухфазные, трехфазные и т.д. системы.
Каждая система состоит из одного или нескольких веществ, называемых компонентами.
Компоненты – индивидуальные вещества, из которых состоит система, и которые могут быть выделены из системы и существовать вне ее.
Числом независимых компонентов называется наименьшее число индивидуальных веществ, необходимое для образования данной системы. Оно равно общему числу индивидуальных веществ, входящих в данную систему, за вычетом числа уравнений, связывающих эти вещества.
По числу компонентов различают однокомпонентные, двухкомпонентные, трехкомпонентные и т.д. системы.
Любая система характеризуется внешними и внутренними параметрами состояния.
Число независимых термодинамических параметров данной системы, производное изменение которых в определенных пределах не вызывает исчезновения одних и образование других фаз называется числом термодинамических степеней свободы, или вариантностью, системы.
По числу термодинамических степеней свободы системы разделяются на инвариантные (С = 0), моновариантные (С = 1), дивариантные (С = 2) и т.д.
Растворомназывается гомогенная однофазная система, состоящая не менее чем из двух независимых компонентов, в каждом элементарном объеме которого одинаковые физические, химические и термодинамические свойства.
Растворителемобычно считают вещество, количество которого в растворе больше или которое не меняет своего агрегатного состояния при образовании раствора, остальные компоненты называют растворенными.
Различают твердые, жидкие и газообразные идеальныеи реальные растворы.
Идеальнымназывается такой раствор, все компоненты которого характеризуются одинаковой формой и размером молекул и одинаковой энергией межмолекулярных взаимодействий.
Идеальные растворы встречаются довольно редко. Это гомогенные смеси близких по физико-химическим свойствам веществ. Например, смеси оптических изомеров, соседних членов одного и того же гомологического ряда. Моделью идеального газового раствора является смесь идеальных газов. Часто к идеальным растворам относят бесконечно разбавленные растворы.
Большинство растворов являются реальными.
Реальные растворы – это растворы, компоненты которых отличаются либо по форме либо по размерам либо по энергии межмолекулярных взаимодействий.
Все свойства растворов подразделяют на экстенсивные и интенсивные.
Экстенсивные свойства – свойства, зависящие как от общей массы раствора, таки от его состава, например V, U, H, G, S, Cp.
Эти свойства относятся ко всему раствору, как единому целому, а не к отдельным его компонентам.
Интенсивныесвойства – это такие свойства, которые зависят только от состава раствора и не зависят от его общей массы, например, давление насыщенного пара.
Для характеристики растворов используют средние мольные и парциальные мольныесвойства.
Среднее мольное свойство – экстенсивное свойство 1 моль раствора.
Например, средний мольный объем можно рассчитать по формуле:
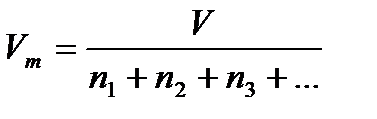 ,
,
где n1, n2, n3,… – число моль первого, второго, третьего и т.д. компонентов.
Парциальное мольное свойствоi-го компонента – это частная производная от экстенсивного свойства раствора по числу молей этого компонента (ni) при постоянстве количества всех остальных компонентов и внешних параметрах (Р и Т).
Парциальное мольное свойство является характеристикой отдельного компонента системы, т.е. является интенсивным свойством раствора.
Например, парциальный мольный объем i-го компонента – это частная производная
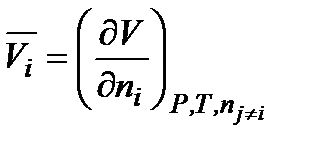 .
.
Дата добавления: 2016-06-22; просмотров: 2253;











