Химический потенциал

Свободная энергия системы (энергия Гиббса G и энергия Гельмгольца F) зависит от внешних условий:

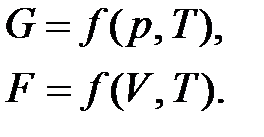
Эта зависимость является полной для простейших систем, состоящих из одного компонента.

Термодинамическая система может состоять как из одного, так и из нескольких компонентов. Очевидно, что величина свободной энергии многокомпонентной системы будет зависеть как от внешних условий (Т, р, или V), так и от природы и количества веществ, составляющих систему, т. е. свободная энергия, как и любая термодинамическая функция, является экстенсивным свойством системы.В случае, если состав системы изменяется во времени (т.е. в системе протекает химическая реакция), необходимо учесть влияние изменения состава на величину свободной энергии системы.

Рассмотрим термодинамическую систему, состоящую из k компонентов. Пусть n₁, n₂, …, n_k – число моль 1-го, 2-го, …, k-го компонентов. Тогда свободная энергия Гиббса является функцией следующих переменных:

G = f(p, T, n₁, n₂, …, n_k)

Продифференцируем по всем переменным:

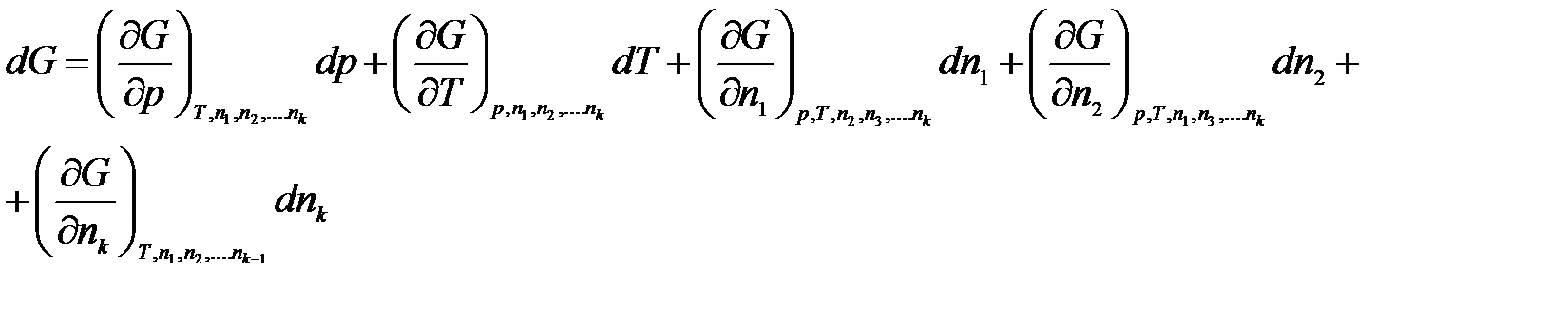(2.1)

Введем обозначение:

………………….

,

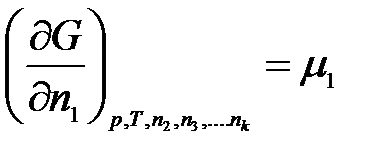
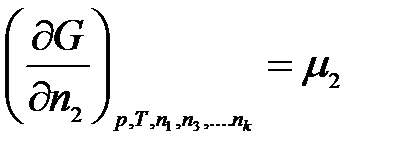
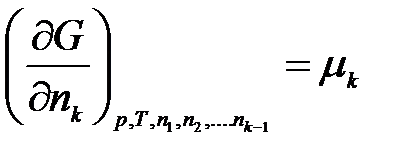где μ₁, μ₂, …, μ_k – химические потенциалы 1-го, 2-го, …, k-го компонентов соответственно.

В общем виде

.

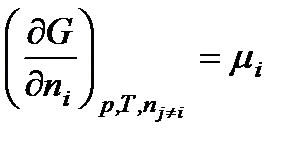Аналогичное выражение получаем для свободной энергии Гельмгольца:

F = f(V, T, n₁, n₂, …, n_k)

.

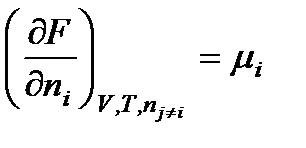Таким образом, химический потенциал – это частная производная от свободной энергии по количеству моль i-го компонента при постоянстве соответствующих внешних параметрах и числе моль всех остальных компонентов. Таким образом, химический потенциал является парциальной мольной энергией Гиббса (при р, Т = const):

.

Свободная энергия – это общее свойство системы, химический потенциал характеризует свойства отдельного компонента, входящего в систему. Химический потенциал является интенсивным свойством системы, т.к. не зависит от массы системы.

При р, Т = const уравнение (2.1) имеет вид:

;

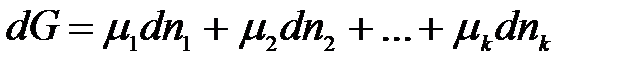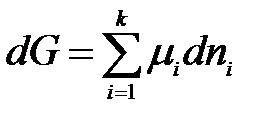. (2.2)

В этом случае изменение энергии Гиббса, то есть полезная работа системы, обусловлена только изменением состава системы в результате протекания химической реакции или вследствие обмена веществом между системой и окружающей средой.

Уравнение (2.2) выражает взаимосвязь между общим свойством системы и свойствами каждого ее компонента. Приняв, что химический потенциал является постоянной величиной, проинтегрируем уравнение (2.2):

.

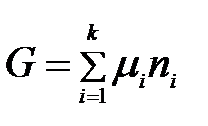Константа интегрирования равна нулю, поскольку, если все n_i = 0, энергия Гиббса также равна нулю.

Для индивидуального вещества

,

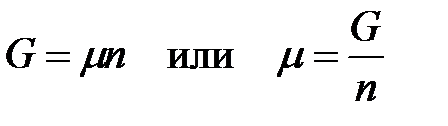т.е. химический потенциал индивидуального вещества равен мольной энергии Гиббса.

При равновесии dG = 0 и уравнение (2.1) принимает вид:

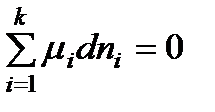. (2.3)

Полученное уравнение является общим условием равновесия в системе с переменным составом при р, Т = const.