Основные характеристики постоянного электрического тока: величина /сила/ тока, плотность тока. Сторонние силы

Скалярная физическая величина, которая показывает, какой заряд переносится носителями через рассматриваемую поверхность (например, через поперечное сечение проводника) в единицу времени, называется величиной (силой) тока:

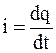. (5.1)

В системе СИ сила тока измеряется в амперах (А). Ампер - это сила такого электрического тока, который, проходя по двум прямолинейным бесконечным проводникам, расположенным на расстоянии 1 м друг от друга, вызывает на каждом участке длиной 1 м силу взаимодействия 2×10^-7 Н.

Векторная физическая величина, численно равная силе тока через площадку dS, перпендикулярную направлению движения электрических зарядов (электрического тока), называется плотностью тока:

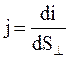. (5.2)

Плотность тока – векторная величина. За направление вектора плотности электрического тока j принимается направление вектора скорости упорядоченного движения положительных зарядов.

Зная вектор плотности тока j в любой точке проводника, можно определить величину тока через любую поверхность:

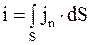, (5.3)

где j_n = j×cosa – проекция вектора плотности тока на направление тока;

a – угол между векторами j и n (положительной нормали к площадке dS).

Таким образом, сила тока через какую-либо поверхность является потоком вектора плотности тока через поверхность.

Если имеется некоторый объем проводника V, ограниченный поверхностью S, то выражение 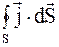определяет заряд, выходящий из объема V в единицу времени. При этом скорость убывания заряда, находящегося в данном объеме (на основании закона сохранения заряда),

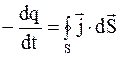, (5.4)

где .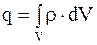

Подставляя значение заряда в формулу (5.4) получим

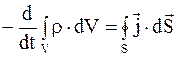или

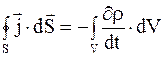. (5.5)

Преобразуем левую часть выражения (5.5) по теореме Остроградского-Гаусса ( ):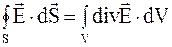

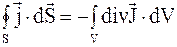. (5.6)

Следовательно, имеем

.

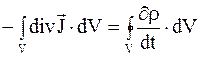Откуда

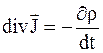. (5.7)

Соотношение (5.7) является уравнением непрерывности для вектора плотности электрического тока. Оно выражает закон сохранения электрических зарядов.

Уравнение непрерывности вектора плотности электрического тока позволяет ввести (по аналогии с линиями вектора напряженности электрического поля E) линии вектора плотности электрического тока. Так как для стационарного (постоянного) тока

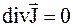, (5.8)

то можно утверждать, что линии вектора плотности электрического тока всегда замкнуты (рис. 5.1).

При наличии тока в проводнике j ¹0 и, следовательно, E ¹ 0. Таким образом, внутри проводника с током имеется электрическое поле (в электростатике поле внутри проводника нет). Кроме того, плотность постоянного тока по сечению проводника распределена неравномерно.

Вблизи поверхности проводника плотность тока может быть направлена только по касательной к поверхности проводника. Это означает, что и напряженность электрического поля E вблизи поверхности проводника направлена по касательной к его поверхности. Что касается эквипотенциальных поверхностей, то они перпендикулярны поверхности проводника. При этом эквипотенциальные поверхности изогнутых проводников не могут находиться на неизменном расстоянии друг от друга во всех точках проводника. Например, в кольцевом проводнике круглого сечения расстояние между эквипотенциальными поверхностями на внутренней части кольца меньше, чем на внешней. Так как расстояние между соседними эквипотенциальными поверхностями изменяется, то изменяется и напряженность электрического поля в соответствующих точках эквипотенциальных поверхностей. А это и означает, что плотность тока в однородных проводниках изменяется по сечению.

Надо отметить, что в круговом проводнике цилиндрической формы бесконечной длины (в линейном проводнике) эквипотенциальные поверхности внутри проводника представляют собой плоскости, перпендикулярные оси проводника. Поэтому по сечению такого проводника плотность электрического тока и напряженность электрического поля постоянны.

Таким образом, вблизи поверхности вне проводника имеется электрическое поле, тангенциальная составляющая вектора напряженности E_i которого равна тангенциальной составляющей вектора напряженности электрического поля внутри проводника (рис. 5.2).

В однородных проводниках первого рода источником электрического поля являются поверхностные заряды. Поверхностная плотность этих зарядов

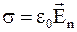, (5.9)

где E_n – нормальная составляющая вектора напряженности электрического поля вблизи его поверхности.

В общем случае силовые линии электрического поля – не касательные к поверхности проводника. Это означает, что наряду с тангенциальной составляющей вектора напряженности электрического поля вблизи поверхности проводника имеется также нормальная составляющая вектора E(рис. 5.3). При этом внутри проводника E_n = 0. Поверхностная плотность электрических зарядов на различных участках проводника может быть как положительной, так и отрицательной.

В неоднородных проводниках проводимость проводников может изменяться от точки к точке в объеме проводника. В стационарном случае 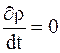, а 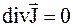, где объемная плотность зарядов, равная сумме объемной плотности свободных зарядов r₁ и объемной плотности связанных зарядов r_св,

.

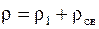Тогда

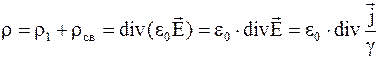, (5.10)

где g – удельная проводимость проводника.

Учитывая выражение 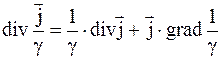, имеем

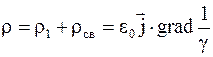. (5.11)

Направляя ось X вдоль прямолинейного участка проводника и считая, что его свойства изменяются только в этом направлении, формулу (5.11) можно переписать в виде

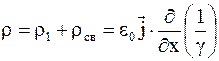. (5.12)

Если проводимость проводника уменьшается в направлении тока проводимости, то объемная плотность заряда положительна. Это связано с тем, что при постоянной площади сечения проводника плотность тока должна быть постоянной, поэтому для поддержания постоянства тока необходимо увеличивать напряженность электрического поля. Увеличение напряженности электрического поля обеспечивается объемными положительными зарядами.

Аналогично можно объяснить возникновение отрицательных объемных зарядов при увеличении проводимости проводника в направлении тока.

Ток, не изменяющийся по величине и направлению с течением времени, называют постоянным.

Для постоянного электрического тока

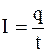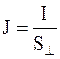; . (5.13)

Существование постоянного тока в проводниках возможно при наличии сторонних сил, которые не могут иметь электростатическое происхождение. Это связано с тем, что электростатическое поле является потенциальным. Следовательно, работа, совершаемая электростатическими силами по замкнутому контуру, в котором существует ток, равна нулю, т. е. при этих условиях существование электрического тока в проводнике невозможно, так как он должен совершать работу по преодолению электрического сопротивления проводника. Существование тока в проводниках доказывает, что сторонние силы имеют не электростатическое происхождение.

Сторонние силы могут быть любой природы, например механической или электрической (сила, действующая на заряд в электрическом поле, возникающем по закону электромагнитной индукции).

Схема простейшего источника тока, в котором сторонняя сила (сторонняя ЭДС) имеет механическое происхождение, представлена на рис. 5.4.

Между электродами ¢А¢ и ¢В¢ имеется нейтральна среда с равным числом положительных и отрицательных зарядов. Сторонняя сила неэлектростатического происхождения перемещает положитель-ные заряды к электроду ¢В¢, а отрицательные – к электроду ¢А¢. В результате этого электрод ¢А¢ заряжается отрицательно, а электрод ¢В¢ - положительно. Во внешней цепи от ¢В¢ к ¢А¢ течет электрический ток, совершающий соответствующую работу. Необходимая для этого энергия сообщается системе сторонними силами, которые совершают работу по разделению электрических зарядов между электродами ¢А¢ и ¢В¢ и доставку этих зарядов на электроды против сил электрического поля с напряженностью E, существующего между электродами. Ток между электродами ¢А¢ и ¢В¢ внутри источника замыкает ток во внешней цепи. Если направление тока рассматривать относительно электродов, то во внешней цепи ток течет от положительного электрода к отрицательному электроду, а внутри источника – от отрицательного электрода к положительному.

Таким образом, сторонние силы разделяют электрические заряды в источниках тока, действуют против кулоновских сил, связывающих разноименные заряды, и характеризуются той работой, которую способны совершить против сил электрического поля внутри источника и против механических сил сопротивления в источнике:

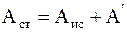, (5.14)

где A_ст – работа сторонних сил;

A_ис – работа сторонних сил против механических сил сопротивления;

A^' – работа сторонних сил против кулоновских сил.

Выражение (5.14) отображает закон сохранения энергии для источника тока. Работа сторонних сил A_ис равна работе, совершаемой электрическими силами вне источника. Следовательно, источник тока является источником той энергии, которая выделяется во внешнем (по отношению к источнику) участке цепи, тем самым создает разность потенциалов на концах проводника. Для поддержания постоянной разности потенциалов в источнике тока должна непрерывно совершаться работа A_ис, которая компенсирует потерю энергии во внешней цепи.

5.3. Электродвижущая сила (ЭДС), напряжение
и разность потенциалов. Их физический смысл.
Связь между ЭДС, напряжением и разностью потенциалов

Физическая величина, равная работе сторонних сил по перемещению положительного единичного заряда вдоль всей цепи, включая источник тока, называется электродвижущей силой источника тока (ЭДС) :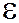

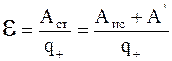. (5.15)

Работа сторонних сил вдоль замкнутой цепи

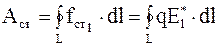, (5.16)

где E^* – напряженность поля сторонних сил.

Тогда

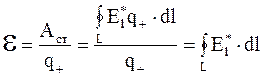. (5.17)

При движении зарядов в проводнике кроме сторонних сил на них действуют силы электростатического поля ( 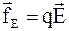). Следовательно, в любой точке цепи на заряд q действует результирующая сила:

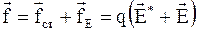. (5.18)

Работа, совершаемая этой силой на участке 1 – 2,

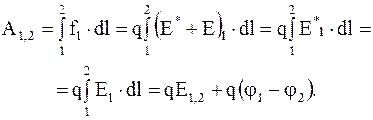(5.19)

Физическая величина, численно равная работе сторонних и электрических сил по перемещению положительного единичного заряда на данном участке цепи, называется падением напряжения или напряжением на данном участке цепи:

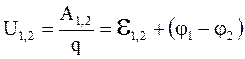. (5.20)

Если на участке цепи отсутствует ЭДС ( 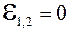), то

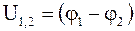. (5.21)

При j₁ - j₂ = 0,

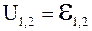. (5.22)

Измеряются e, U, (j₁ - j₂) в системе СИ в вольтах (1 В).

Лекция 6. Классическая электронная теория
проводимости металлов. Законы постоянного тока

Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Ома в дифференциальной и интегральной формах. Электрическое сопротивление проводников. Изменение сопротивления проводников от температуры и давления. Сверхпроводимость. Соединения сопротивлений: последовательное, параллельное, смешанное. Шунтирование электроизмерительных приборов. Добавочные сопротивления к электроизмерительным приборам. Правила (законы) Кирхгофа и их применение к расчету простейших электрических цепей. Закон Джоуля-Ленца в дифференциальной и интегральной формах. Энергия, выделяющаяся в цепи постоянного тока. Коэффициент полезного действия (КПД) источника постоянного тока.

6.1. Классическая электронная теория электропроводности металлов и ее опытные обоснования.
Закон Ома в дифференциальной и интегральной формах

Классическая электронная теория проводимости металлов объясняет различные электрические свойства веществ существованием и движением в них так называемых квазисвободных электронов проводимости. Электроны проводимости при этом рассматриваются как электронный газ, подобный идеальному газу молекулярной физики.

До открытия электронов было экспериментально показано, что прохождение тока в металлах не связано, в отличие от тока в жидких электролитах, с переносом вещества металла. Опыт состоял в том, что через контакт двух различных металлов, например золота и серебра, в течение времени, исчисляемого многими месяцами, пропускали электрический ток. После чего исследовался материал вблизи контактов. Было показано, что никакого переноса вещества через границу различных металлов не наблюдается и вещество по различные стороны границы раздела имеет тот же состав, что и до пропускания тока. Опыты доказали, что атомы и молекулы металлов не принимают участия в переносе электрического тока, но они не ответили на вопрос о природе носителей заряда в металлах.

Прямым доказательством, что электрический ток в металлах обусловливается движением электронов, были опыты Толмена и Стюарда, проведенные в 1916 г. Идея этих опытов была высказана Мандельштамом и Папалекси в 1913 г.

Представим себе проводящую катушку, которая может вращаться вокруг своей оси. Концы катушки с помощью скользящих контактов замкнуты на гальванометр. Если находящуюся в быстром вращении катушку резко затормозить, то свободные электроны в проволоке продолжают движение по инерции, в результате чего гальванометр должен зарегистрировать импульс тока.

Обозначим линейное ускорение катушки при торможении –a. Оно направлено по касательной к поверхности катушки. При достаточно плотной намотке и тонких проводах можно считать, что ускорение направлено вдоль проводов. При торможении катушки к каждому свободному электрону приложена сила инерции F_ин = m_e×a, направленная противоположно ускорению. Под ее действием электрон ведет себя в металле так, как если бы на него действовало эффективное электрическое поле с напряженностью

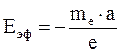. 6.1)

Поэтому эффективная электродвижущая сила в катушке, обусловленная инерцией свободных электронов,

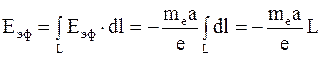, (6.2)

где L – длина провода на катушке.

Все точки провода тормозятся с одинаковым ускорением, и поэтому ускорение вынесено за знак интеграла.

С учетом формулы (6.2) запишем закон Ома для замкнутой цепи в виде

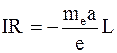, (6.3)

где I – сила тока в замкнутой цепи;

R – сопротивление всей цепи, включая сопротивление проводов катушки, проводов внешней цепи и гальванометра.

Количество электричества, протекшее через поперечное сечение проводника в течение времени dt при силе тока I,

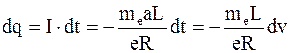. (6.4)

Поэтому в течение времени торможения катушки от начальной линейной скорости v_o до полной остановки через гальванометр пройдет количество электричества

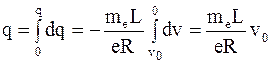. (6.5)

Значение q определяется по гальванометру, а значения L, R, v_o известны. Поэтому можно найти как знак, так и абсолютное значение e/m_e. Эксперименты показали, что e/m_e соответствует отношению заряда электрона к его массе. Таким образом, было доказано, что наблюдаемый с помощью гальванометра ток обусловлен движением электронов.

В отсутствие электрического поля в проводниках электроны проводимости движутся хаотично, в произвольных направлениях со скоростями, обусловленными температурой, т.е. с так называемой тепловой скоростью u.

Через определенный промежуток времени t = t, двигаясь по прямой, электрон проводимости может провзаимодействовать с ионом кристаллической решетки или с другим электроном проводимости. В результате такого взаимодействия, а оно считается в классической теории проводимости абсолютно упругим, сохраняются полные импульс и энергия, а величина и направление скорости движения могут измениться. Предельным является случай, когда через время, равное t (время свободного пробега), направление скорости теплового движения электрона проводимости изменяется на противоположное. Время свободного пробега зависит от природы вещества и тем меньше, чем чаще происходят взаимодействия. Между соударениями (взаимодействиями) со скоростью u ничего не происходит.

При наложении электричес-кого поля с напряженностью E под действием силы F = e×E электроны проводимости приоб-ретают некоторое ускорение a и направленное движение с изменяющейся скоростью от v_o =0 до v = v_max за время t = t.

Изменение скорости направленного движения электрона проводимости происходит до его взаимодействия (рис. 6.1). В результате взаимодействия эта скорость так же может измениться как по величине, так и по направлению.

Если в единице объема проводника n электронов проводимости, которые в некоторый момент времени t обладают скоростью v, то можно определить заряд, прошедший через некоторую площадку S, расположенную перпендикулярно направлению скорости движения электронов проводимости:

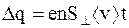, (6.6)

где <v> - средняя скорость упорядоченного движения электронов проводимости.

Сила (величина) тока в проводнике в этом случае

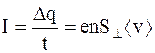. (6.7)

Плотность тока проводимости

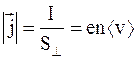. (6.8)

В векторной форме

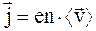. (6.9)

Согласно (6.8) для определения плотности электрического тока в проводнике необходимо определить среднюю скорость упорядоченного движения электронов проводимости.

Средняя скорость упорядоченного движения в данном случае может быть определена по формуле

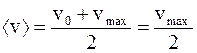, (6.10)

т.к. в начальный момент времени t=0, когда отсутствует электрическое поле, v_o=0.

Максимальная скорость упорядоченного движения, которую приобретает электрон под действием электрического поля за время свободного пробега,

,

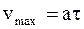где a – ускорение, приобретаемое электроном проводимости под действием электрического поля;

t – время пробега электрона проводимости от взаимодействия до взаимодействия.

На основании второго закона Ньютона F = m×a, где F - кулоновская сила,

F = eE.

Имеем:

;

;

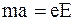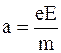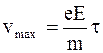. (6.11)

Для средней скорости упорядоченного движения электронов проводимости получим

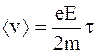. (6.12)

Зная среднюю скорость теплового движения электронов проводимости и среднее расстояние, проходимое ими от взаимодействия до взаимодействия, можно определить время между двумя последующими взаимодействиями:

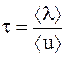. (6.13)

Сделав подстановку и необходимые преобразования, для плотности тока проводимости будем иметь

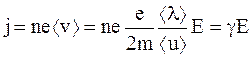, (6.14)

где 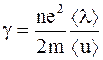- удельная электропроводность металла проводника.

В векторной форме

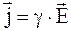. (6.15)

Выражения (6.14) и (22.15) являются математической формой записи закона Ома в дифференциальной форме.

Закон Ома в дифференциальной форме справедлив для любых проводников, любых токов, характеризует плотность тока проводимости в любой точке проводника.

Из закона Ома в дифференциальной форме можно получить закон Ома в интегральной форме для замкнутой (или полной) цепи. Для чего выражение (6.15) умножим на величину элементарного участка цепи dl:

,

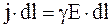где ; ; .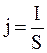

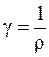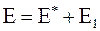Таким образом, имеем

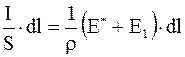
или

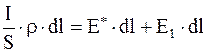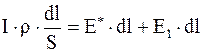; . (6.16)

Проинтегрировав выражение (6.16) по замкнутому контуру L, получим

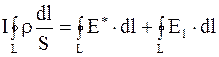, (6.17)

где 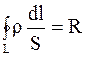– сопротивление внешнего и внутреннего участков цепи;

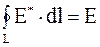– ЭДС, действующая в замкнутой цепи, численно равная циркуляции вектора напряженности поля сторонних сил;

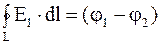– разность потенциалов между двумя рассматриваемыми точками замкнутой цепи.

Для замкнутой цепи

(j₁ - j₂) = 0; .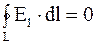

Таким образом, имеем

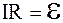или 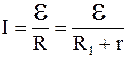, (6.18)

где R₁ – сопротивление внешнего участка цепи;

r – внутреннее сопротивление источника тока.

Из формулы (6.18)

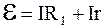. (6.19)

Следовательно, ЭДС уравновешивает падение напряжения во внешней и внутренней цепи и тем самым обеспечивает непрерывное движение электронов проводимости.

Если цепь не замкнута и в ней отсутствует ЭДС, то

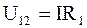, а 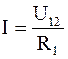. (6.20)

Выражения (6.18) и (6.20) являются математической формой записи закона Ома, соответственно, для полной (замкнутой) цепи и участка цепи, который был открыт им экспериментально. Сила тока в цепи прямопропорциональна ЭДС (напряжению на участке цепи) и обратно пропорциональна сопротивлению цепи.

6.2. Электрическое сопротивление проводников.
Изменение сопротивления проводников от температуры
и давления. Сверхпроводимость

Из выражения 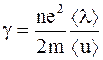видно, что удельная электропроводимость проводников, а следовательно, удельное электросопротивление и сопротивление зависят от материала проводника и его состояния. Состояние проводника может изменяться в зависимости от различных внешних факторов давления (механических напряжений, внешних сил, сжатия, растяжения и т.д., т.е. факторов, влияющих на кристаллическое строение металлических проводников) и температуры.

Электрическое сопротивление проводников (сопротивление) зависит от формы, размеров, материала проводника, давления и температуры:

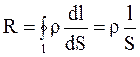. (6.21)

При этом зависимость удельного электрического сопротивления проводников и сопротивления проводников от температуры, как было установлено экспериментально, описывается линейными законами:

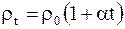; (6.22)

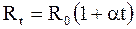, (6.23)

где r_t и r_o, R_t и R_o - соответственно удельные сопротивления и сопротивления проводника при t = 0 ^oC;

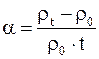или 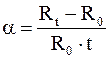. (6.24)

Из формулы (6.23) температурная зависимость сопротивления проводников

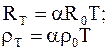, (6.25)

где T – термодинамическая температура.

График зависимости сопротивления проводников от температуры представлен на рис. 6.2. График зависимости удельного сопротивления r металлов от абсолютной температуры T представлен на рис. 6.3.

Согласно классической электронной теории металлов в идеальной кристаллической решетке (идеальном проводнике) электроны движутся, не испытывая электрического сопротивления (r = 0). С точки зрения современных представлений, причинами, вызывающими появление электрического сопротивления в металлах, являются посторонние примеси и дефекты кристаллической решетки, а также тепловое движение атомов металла, амплитуда которых зависит от температуры.

Правило Матиссена утверждает, что зависимость удельного электрического сопротивления от температуры r(T) является сложной функцией, которая состоит из двух независимых слагаемых:

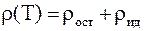, (6.26)

где r_ост – остаточное удельное сопротивление;

r_ид – идеальное удельное сопротивление металла, которое соответствует сопротивлению абсолютно чистого металла и определяется лишь тепловыми колебаниями атомов.

На основании формул (6.25) удельное сопротивление идеального металла должно стремиться к нулю, когда T ® 0 (кривая 1 на рис. 6.3). Однако удельное сопротивление как функция температуры является суммой независимых слагаемых r_ид и r_ост. Поэтому в связи с наличием примесей и других дефектов кристаллической решетки металла удельное сопротивление r(T) при понижении температуры стремится к некоторой постоянной конечной величине r_ост (кривая 2 на рис. 6.3). Иногда переходя минимум, несколько повышается при дальнейшем понижении температуры (кривая 3 на рис. 6.3). Величина остаточного удельного сопротивления зависит от наличия дефектов в решетке и содержания примесей, возрастает при увеличении их концентрации. Если количество примесей и дефектов кристаллической решетки свести к минимуму, то остается еще один фактор, влияющий на электрическое удельное сопротивление металлов, - тепловое колебание атомов, которое, как утверждает квантовая механика, не прекращается и при температуре абсолютного нуля. В результате этих колебаний решетка перестает быть идеальной, и в пространстве возникают переменные силы, действие которых приводит к рассеянию электронов, т.е. возникновению сопротивления.

В последствии было обнаружено, что сопротивление некоторых металлов (Al, Pb, Zn и др.) и их сплавов при низких температурах T (0,14¸20 К), называемых критическими, характерных для каждого вещества, скачкообразно уменьшается до нуля, т.е. металл становится абсолютным проводником. Впервые это явление, называемое сверхпроводимостью, обнаружено в 1911 г. Г. Камерлинг-Оннесом для ртути. Было обнаружено, что при Т = 4,2 К ртуть, по-видимому, полностью теряет сопротивление электрическому току. Уменьшение сопротивления происходит очень резко в интервале нескольких сотых градуса. В дальнейшем потеря сопротивления наблюдалась и у других чистых веществ и у многих сплавов. Температуры перехода в сверхпроводящее состояние различны, но всегда очень низки.

Возбудив электрический ток в кольце из сверхпроводящего материала (например, с помощью электромагнитной индукции), можно наблюдать, что его сила в течение нескольких лет не уменьшается. Это позволяет найти верхний предел удельного сопротивления сверхпроводников (менее 10^-25 Ом×м), что гораздо меньше, чем удельное сопротивление меди при низкой температуре (~10^-12 Ом× м). Поэтому принимается, что электрическое сопротивление сверхпроводников равно нулю. Сопротивление до перехода в сверхпроводящее состояние бывает самым различным. Многие из сверхпроводников при комнатной температуре имеют довольно высокое сопротивление. Переход в сверхпроводящее состояние совершается всегда очень резко. У чистых монокристаллов он занимает интервал температур меньший, чем одна тысячная градуса.

Сверхпроводимостью среди чистых веществ обладают алюминий, кадмий, цинк, индий, галлий. В процессе исследований оказалось, что структура кристаллической решетки, однородность и чистота материала оказывают значительное влияние на характер перехода в сверхпроводящее состояние. Это видно, например, на рис. 6.4, на котором приведены экспериментальные кривые перехода в сверхпроводящее состояние олова различной чистоты (кривая 1 – монокристаллическое олово; 2 – поликристаллическое олово; 3 – поликристаллическое олово с примесями).

В 1914 г. К. Оннес обнаружил, что сверхпроводящее состояние разрушается магнитным полем, когда магнитная индукция B превосходит некоторое критическое значение. Критическое значение индукции зависит от материала сверхпроводника и температуры. Критическое поле, разрушающее сверхпроводимость, может быть создано и самим сверхпроводящим током. Поэтому имеется критическая сила тока, при которой сверхпроводимость разрушается.

В 1933 г. Мейсснер и Оксенфельд обнаружили, что внутри сверхпроводящего тела полностью отсутствует магнитное поле. При охлаждении сверхпроводника, находящегося во внешнем постоянном магнитном поле, в момент перехода в сверхпроводящее состояние магнитное поле полностью вытесняется из его объема. Этим сверхпроводник отличается от идеального проводника, у которого при падении удельного сопротивления до нуля индукция магнитного поля в объеме должна сохраняться без изменения. Явление вытеснения магнитного поля из объема проводника называется эффектом Мейсснера. Эффект Мейсснера и отсутствие электрического сопротивления являются важнейшими свойствами сверхпроводника.

Отсутствие магнитного поля в объеме проводника позволяет заключить из общих законов магнитного поля, что в нем существует только поверхностный ток. Он физически реален и поэтому занимает некоторый тонкий слой вблизи поверхности. Магнитное поле тока уничтожает внутри проводника внешнее магнитное поле. В этом отношении сверхпроводник ведет себя формально как идеальный диамагнетик. Однако он не является диамагнетиком, поскольку внутри его намагниченность (вектор намагничивания) равна нулю.

Чистые вещества, у которых наблюдается явление сверхпроводимости, немногочисленны. Чаще сверхпроводимость наблюдается у сплавов. У чистых веществ имеет место только эффект Мейсснера, а у сплавов не происходит полного выталкивания магнитного поля из объема (наблюдается частичный эффект Мейсснера).

Вещества, в которых наблюдается полный эффект Мейсснера, называются сверхпроводниками первого рода, а частичный – сверхпроводниками второго рода.

У сверхпроводников второго рода в объеме имеются круговые токи, создающие магнитное поле, которое, однако, заполняет не весь объем, а распределено в нем в виде отдельных нитей. Что же касается сопротивления, то оно равно нулю, как и у сверхпроводников первого рода.

По своей физической природе сверхпроводимость является сверхтекучестью жидкости, состоящей из электронов. Сверхтекучесть возникает из-за прекращения обмена энергией между сверхтекучей компонентой жидкости и ее другими частями, в результате чего исчезает трение. Существенным при этом является возможность "конденсации" молекул жидкости на низшем энергетическом уровне, отделенном от других уровней достаточно широкой энергетической щелью, которую силы взаимодействия не в состоянии преодолеть. В этом и состоит причина выключения взаимодействия. Для возможности нахождения на низшем уровне многих частиц необходимо, чтобы они подчинялись статистике Бозе-Эйнштейна, т.е. обладали целочисленным спином.

Электроны подчиняются статистике Ферми-Дирака и поэтому не могут "конденсироваться" на низшем энергетическом уровне и образовывать сверхтекучую электронную жидкость. Силы отталкивания между электронами в значительной степени компенсируются силами притяжения положительных ионов кристаллической решетки. Однако благодаря тепловым колебаниям атомов в узлах кристаллической решетки между электронами может возникнуть сила притяжения, и они тогда объединяются в пары. Пары электронов ведут себя как частицы с целочисленным спином, т.е. подчиняются статистике Бозе-Эйнштейна. Они могут конденсироваться и образовывать ток сверхтекучей жидкости электронных пар, который и образует сверхпроводящий электрический ток. Выше низшего энергетического уровня имеется энергетическая щель, которую электронная пара не в состоянии преодолеть за счет энергии взаимодействия с остальными зарядами, т.е. не может изменить своего энергетического состояния. Поэтому электрическое сопротивление отсутствует.

Возможность образования электронных пар и их сверхтекучести объясняется квантовой теорией.

Практическое использование сверхпроводящих материалов (в обмотках сверхпроводящих магнитов, в системах памяти ЭВМ и др.) затруднено из-за низких их критических температур. В настоящее время обнаружены и активно исследуются керамические материалы, обладающие сверхпроводимостью при температурах выше 100 К (высокотемпературные сверхпроводники). Явление сверхпроводимости объясняется квантовой теорией.

Зависимость сопротивления проводников от температуры и давления используется в технике для измерения температуры (термометры сопротивления) и больших быстроизменяющихся давлений (электрические тензометры).

В системе СИ удельное электрическое сопротивление проводников измеряется в Ом×м, а сопротивление – в Ом. Один Ом – сопротивление такого проводника, в котором при напряжении 1В течет постоянный ток силой 1А.

Электрической проводимостью называется величина, определяемая по формуле

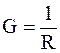. (6.27)

В системе СИ единицей проводимости является сименс. Один сименс (1 См) – проводимость участка цепи сопротивлением 1 Ом.

6.3. Соединения сопротивлений: последовательное, параллельное, смешанное.
Шунтирование электроизмерительных приборов.
Добавочные сопротивления к электроизмерительным приборам