Основные уравнения электростатики диэлектриков

Условие нейтральности объема V имеет вид

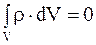. (3.29)

Дипольный момент для двух точечных зарядов

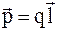. (3.30)

При непрерывном распределении зарядов электрический дипольный момент определяется формулой

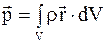, (3.31)

где r – радиус-вектор, который отсчитывается от любой точки.

Напряженность и потенциал электрического поля нейтральной системы с дипольным моментом p определяются соотношениями

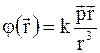; (3.32)

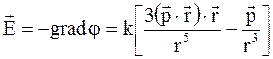. (3.33)

Степень поляризации диэлектриков характеризуется вектором поляризации, определяемым как отношение электрического дипольного момента Dp элемента диэлектрика к его объему DV:

.

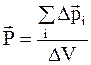При этом вектор поляризации диэлектриков, состоящих из неполярных молекул,

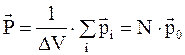, (3.34)

где N – концентрация молекул;

p_o – индуцированный дипольный момент (одинаков у всех молекул), совпадающий по направлению с напряженностью E внешнего электрического поля;

i – символ, который указывает, что суммирование распространяется на все молекулы объема DV.

Для диэлектриков, состоящих из полярных молекул, вектор поляризации

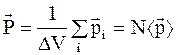, (3.35)

где <p> – среднее значение дипольных моментов, равных друг другу по абсолютному значению, отличающихся направлением.

Диэлектрические свойства линейного изотропного диэлектрика характеризуются одной скалярной величиной - диэлектрической восприимчивостью.

Для такого диэлектрика

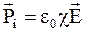, (3.36)

где c – диэлектрическая восприимчивость.

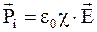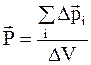Дипольный момент элемента объема dV в соответствии с формулами и равен

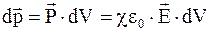. (3.37)

Величина связанных зарядов определяется формулой

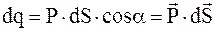. (3.38)

Объемная плотность связанных зарядов, которые возникают лишь в том случае, когда вектор поляризации P изменяется от точки к точке, определяется так:

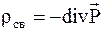. (3.39)

На границе двух различных диэлектриков возникают поверхностные заряды, при этом

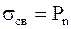, (3.40)

где P_n - нормальная составляющая вектора поляризации диэлектрика на его границе раздела с вакуумом.

Потенциал j_д, создаваемый связанными зарядами диэлектрика, можно определить по формуле

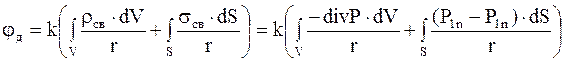. (3.41)

Данный потенциал суммируется с потенциалом, создаваемым свободными зарядами, поверхностная плотность которых

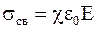, (3.42)

где E – напряженность электрического поля, которая численно равна проекции вектора напряженности на направление внешней нормали к поверхности диэлектрика.

Уравнение 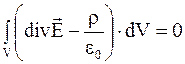с учетом связанных зарядов как источников поля может быть записано, очевидно, следующим образом:

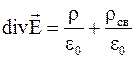. (3.43)

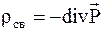
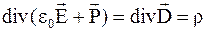, (3.44)

где D = e_oE + P.

Относительная диэлектрическая проницаемость среды

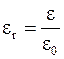. (3.45)

Теорема Остроградского-Гаусса при наличии диэлектриков

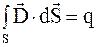. (3.46)