Энергия заряженных проводников, диполя во внешнем электрическом поле, диэлектрического тела во внешнем электрическом поле, заряженного конденсатора

Известно, что во внешнем электрическом поле заряды в объеме проводников отсутствуют. На проводниках имеются только поверхностные заряды. Потенциал в объеме проводников имеет одно и то же значение. Следовательно, формулу для определения энергии системы электрических зарядов

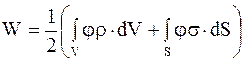
для системы проводников можно записать так:

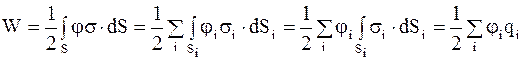. (4.13)

В качестве примера определим энергию электрического поля плоского конденсатора (системы проводников, разделенных слоем диэлектрика).

При сообщении конденсатору электрического заряда dq между его пластинами (обкладками) создается электрическое поле. Сообщенный заряд препятствует дальнейшей зарядке конденсатора. Поэтому для помещения новой порции заряда dq на конденсатор необходимо совершить некоторую работу

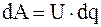. (4.14)

Так как никаких других изменений в конденсаторе, кроме появления электрического поля внутри его, не происходит, то эта работа идет на изменение энергии электрического поля, т.е.

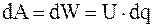, (4.15)

где .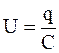

Следовательно,

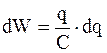. (4.16)

Если конденсатор заряжен полностью, т.е. ему сообщен заряд q, то энергия его электрического поля

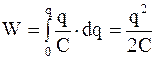. (4.17)

Так как q = CU, то

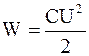. (4.18)

С учетом того что для плоского конденсатора U = Ed, а ,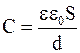

имеем

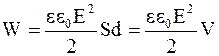, (4.19)

где V = Sd – объем пространства между обкладками конденсатора;

E – напряженность электрического поля;

d – расстояние между пластинами конденсатора;

S – площадь одной из пластин конденсатора.

Энергия электрического поля диполя равна сумме энергий зарядов диполя:

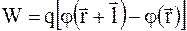. (4.20)

Разложив j(r + l) в ряд Тейлора и ограничившись членами первого порядка по l, получим

.

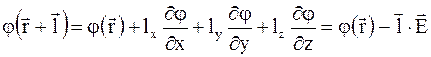Тогда для энергии диполя во внешнем электрическом поле получим

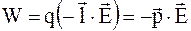. (4.21)

Дипольный момент элемента объема dV тела равен dp = P×dV. Энергия этого элемента во внешнем поле напряженностью E равна

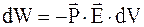. (4.22)

Для определения энергии диэлектрического тела во внешнем электрическом поле необходимо учитывать то, что каждый поляризованный элемент объема dV диэлектрического тела (диполь) становится источником электрического поля. Благодаря чему в расчет энергии электрического поля он должен входить дважды: один раз как диполь, находящийся во внешнем электрическом поле, а другой раз как источник поля, в котором находятся другие диполи.

Поэтому энергия диэлектрика, помещенного во внешнее электрическое поле, равна разности энергии электрического поля, порождаемого некоторой системой электрических зарядов в пространстве, которое заполнено диэлектрической средой, и энергии электрического поля той же системы зарядов, в том же пространстве, но без диэлектрической среды.

Если напряженность электрического поля в отсутствие диэлектрической среды E₀ (D₀ = e₀×E₀), а при наличии диэлектрической среды с напряженностью E (D = ee₀×E), то энергия электрического поля в диэлектрике равна

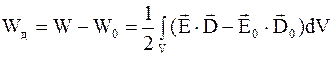, (4.23)

где 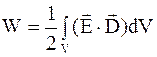– энергия электрического поля при наличии диэлектрика;

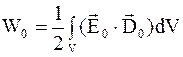– энергия электрического поля в отсутствие диэлектрика.

При заполнении пространства однородным диэлектриком напряженность электрического поля уменьшается в 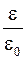раз. Следовательно, 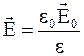и подынтегральное выражение в формуле (4.23) можно привести к виду

,

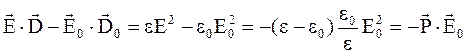где .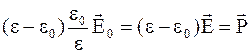

В результате для энергии диэлектрика во внешнем электрическом поле будем иметь

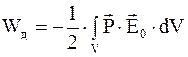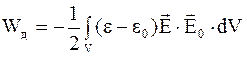или . (4.24)

Воспользовавшись формулой (4.24), можно получить формулу для энергии диэлектрика с проницаемостью e₂, находящегося в среде с диэлектрической проницаемостью e₁.

Запишем формулу для энергии диэлектрика с проницаемостью e₁

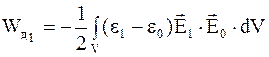, (4.25)

где E₁ – напряженность электрического поля, которое создано системой зарядов в пространстве, заполненном первым диэлектриком;

E₀ – напряженность электрического поля, которое создано системой зарядов в том же пространстве, но не заполненном первым диэлектриком.

Аналогично для диэлектрика с проницаемостью e₂

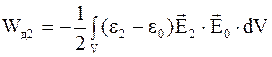. (4.26)

Разность этих энергий

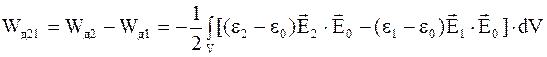. (4.27)

С учетом того что 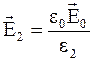, а 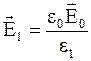, подынтегральное выражение (4.27) можно преобразовать так:

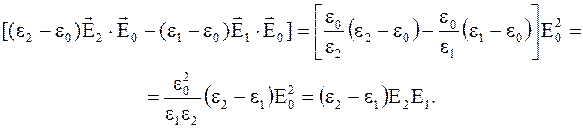
Тогда формула (4.27) примет вид

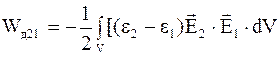, (4.28)

где W_д21 – энергия диэлектрика с диэлектрической проницаемостью e₂, помещенного в диэлектрик (среду) с диэлектрической проницаемостью e₁; поле, с напряженностью E₁, в котором создается свободными фиксированными зарядами.

Из формулы (4.28) следует, что увеличение диэлектрической проницаемости среды ведет к уменьшению полной энергии поля.

4.3. Энергия электрического поля.
Объемная плотность энергии электрического поля

Воспользовавшись уравнением 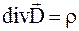, перепишем выражение 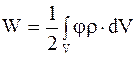в виде

. (4.29)

Так как 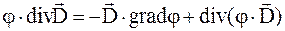, то формулу (4.29) можно записать так:

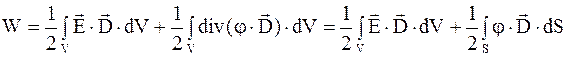, (4.30)

где E = -gradj; 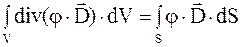– на основании теоремы Остроградского-Гаусса;

S – замкнутая поверхность, охватывающая объем V.

В силу того что при удалении поверхности интегрирования на бесконечность 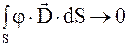, имеем

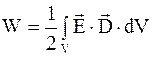. (4.31)

Таким образом, энергию электрического поля можно вычислять по формулам (4.7) или (4.31). Численное значение энергии будет одним и тем же. Однако физическое содержание этих формул различно. Это связано с тем, что в формуле (4.7) носителями энергии выступают заряды и энергия представляется локализованной на зарядах. В формуле (4.31) носителем энергии считается электрическое поле, и энергия представляется локализованной во всем пространстве, где существует электрическое поле.

Под объемной плотностью энергии электрического поля подразумевают энергию единицы объема пространства, в котором существует электрическое поле:

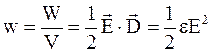. (4.32)

Из выражения (4.32) видно, что объемная плотность энергии электрического всегда положительна, так как 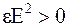. Следовательно, и полная энергия электрического поля всегда положительна.

Однако энергия взаимодействия между дискретными зарядами положительна тогда, когда их собственная энергия (всегда положительная) меньше полной энергии поля, и отрицательна тогда, когда их собственная энергия больше полной энергии электрического поля.

Объемная плотность энергии электрического поля в плоском конденсаторе (электрическое поле однородное)

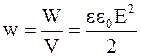. (4.33)

Из формулы (4.33) видно, что объемная плотность энергии электрического поля плоского конденсатора не зависит от его геометрических размеров. Следовательно, объемную плотность энергии неоднородного электрического поля тоже можно рассчитывать по формуле (4.33).

Зная объемную плотность энергии электрического поля, можно рассчитать энергию электрического поля:

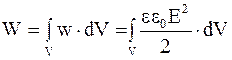. (4.34)

4.4. Силы, действующие на макроскопические
заряженные тела, помещенные в электрическое поле

Пластины конденсаторов, заряженные зарядами противоположного знака, взаимно притягиваются. Механические силы, действующие на макроскопические заряженные тела, называют пондеромоторными.

Как показывают расчеты, величина этих сил не зависит от следующих условий:

а) когда конденсатор заряжен и отключен от источника. В этом случае величина заряда на его пластинах остается постоянной;

б) когда конденсатор заряжен, но не отключен от источника питания. В этом случае напряжение на его обкладках остается постоянным.

Действующие силы могут изменить положение пластин конденсатора на расстояние dx, совершив работу dA = F×dx, которая равна изменению потенциальной энергии, при этом

.

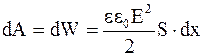Имеем

.

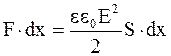Откуда

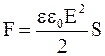. (4.35)

Механические силы действуют не только на пластины конденсатора, но и на диэлектрик, помещенный между ними. В результате диэлектрик деформируется. Поверхности диэлектрика испытывают некоторое давление, величина которого

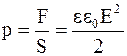. (4.36)

Из выражений (4.33 и 4.36) видно, что плотность энергии электрического поля и давление, создаваемое на поверхность диэлектрика, численно равны. Следовательно, зная плотность энергии электрического поля, можно рассчитать давление и величину механических сил, действующих на макроскопические тела (пондеромоторных сил) в электрическом поле:

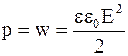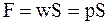; . (4.37)