Энергия взаимодействия электрических зарядов
Силы взаимодействия электрических зарядов консервативны, следовательно, система электрических зарядов обладает потенциальной энергией.
Пусть даны два точечных неподвижных заряда q1 и q2, находящиеся на расстоянии r друг от друга. Каждый из зарядов в поле другого заряда обладает потенциальной энергией
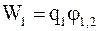 ;
; 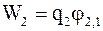 , (4.1)
, (4.1)
где j1,2 и j2,1 – соответственно потенциалы, создаваемые зарядом q2 в точке нахождения заряда q1 и зарядом q1 в точке нахождения заряда q2.
Так как
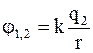 , а
, а 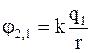 , (4.2)
, (4.2)
то
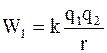 , а
, а 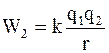 . (4.3)
. (4.3)
Следовательно,
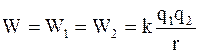 . (4.4)
. (4.4)
Для того чтобы в уравнение энергии системы оба заряда входили симметрично, выражение (4.4) можно записать в виде
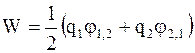 . (4.5)
. (4.5)
Добавляя к системе зарядов последовательно заряды q3, q4 и т.д., можно убедиться, что в случае N зарядов потенциальная энергия системы
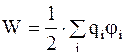 , (4.6)
, (4.6)
где ji – потенциал создаваемый в точке нахождения qi всеми зарядами, кроме i - го.
При непрерывном распределении зарядов в элементарном объеме dV находится заряд dq = r×dV. Для определения энергии взаимодействия заряда dq можно применить формулу (4.6), перейдя в ней от суммы к интегралу:
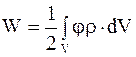 , (4.7)
, (4.7)
где j – потенциал в точке элемента объема dV.
Надо отметить, что между формулами (4.6) и (4.7) существует принципиальное различие. Формула (4.6) учитывает только энергию взаимодействия между точечными зарядами, но не учитывает энергии взаимодействия элементов заряда каждого из точечных зарядов между собой (собственную энергию точечного заряда). Формула (4.7) учитывает как энергию взаимодействия между точечными зарядами, так и собственную энергию этих зарядов. При расчете энергии взаимодействия точечных зарядов она сводится к интегралам по объему Vi точечных зарядов:
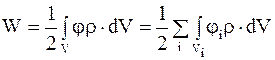 , (4.8)
, (4.8)
где ji - потенциал в любой точке объема i-го точечного заряда;
ji = ji¢ + jiс, (4.9)
где ji¢ - потенциал, созданный другими точечными зарядами в этой же точке;
jiс – потенциал, созданный частями i-го точечного заряда в данной точке.
Так как точечные заряды можно представить сферически симметричными, то
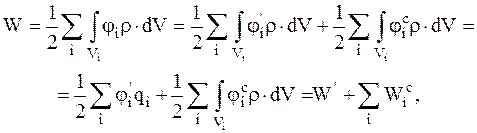 (4.10)
(4.10)
где W¢ определяется по формуле (4.6).
Значение собственной энергии зарядов зависит от законов распределения зарядов и от величины зарядов. Например, при равномерном сферическом распределении зарядов с поверхностной плотностью s
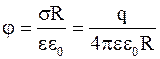 .
.
Следовательно,
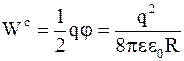 . (4.11)
. (4.11)
Из формулы (4.11) видно, что при R®0 величина Wс®¥. Это означает, что собственная энергия точечного заряда равна бесконечности. Это приводит к серьезным недостаткам понятия "точечный заряд".
Таким образом, формулу (4.6) можно применять для анализа взаимодействия точечных зарядов, поскольку она не содержит их собственной энергии. Формула (4.7) для непрерывного распределения заряда учитывает всю энергию взаимодействия, поэтому является более общей.
При наличии поверхностных зарядов вид формулы (4.7) несколько изменяется. Подынтегральное выражение этой формулы равно 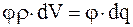 и имеет смысл потенциальной энергии, которой обладает элемент заряда dq, находясь в точке с потенциалом j. Эта потенциальная энергия не зависит от того, является ли dq элементом объемного или поверхностного заряда. Поэтому для поверхностного распределения dq = s×dS. Следовательно, для энергии поля поверхностных зарядов
и имеет смысл потенциальной энергии, которой обладает элемент заряда dq, находясь в точке с потенциалом j. Эта потенциальная энергия не зависит от того, является ли dq элементом объемного или поверхностного заряда. Поэтому для поверхностного распределения dq = s×dS. Следовательно, для энергии поля поверхностных зарядов
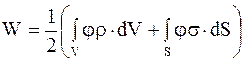 . (4.12)
. (4.12)
Дата добавления: 2016-06-22; просмотров: 5112;











