Поле объёмно заряженного шара
 Дан равномерно заряженный по объёму шар, радиус которого R. Объёмная плотность заряда (при равномерном распределении заряда)
Дан равномерно заряженный по объёму шар, радиус которого R. Объёмная плотность заряда (при равномерном распределении заряда)  . Линии вектора напряженности электрического поля в этом случае направлены по радиальным прямым, перпендикулярно поверхности шара.
. Линии вектора напряженности электрического поля в этом случае направлены по радиальным прямым, перпендикулярно поверхности шара.
Рассчитаем напряженность электрического поля в точке "А", находящейся на расстоянии r>R (рис. 1.19).
Построив замкнутую сферическую поверхность с радиусом r, для потока вектора напряженности электрического поля имеем
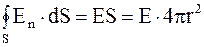 .
.
Заряд, находящийся внутри построенной поверхности,
 .
.
Имеем

 . (1.76)
. (1.76)
Из уравнения (1.75) получим
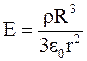 , (1.77)
, (1.77)
где r - объемная плотность заряда;
R – радиус шара;
r – расстояние от рассматриваемой точки поля до центра шара.
Из формулы (1.77) можно сделать выводы:
а) при r = R
 ; (1.78)
; (1.78)
 б) при r<R
б) при r<R
 ; (1.79)
; (1.79)
в) при r = 0
E = 0. (1.80)
График зависимости напряжен-ности электрического поля от расстояния до центра шара представлен на рис. 1.20.
Для решения задачи по определению разности потенциалов между двумя точками такого поля воспользуемся уравнением
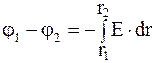 ,
,
где 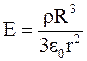 - напряженность поля в точке, расположенной на расстоянии r от центра сферы.
- напряженность поля в точке, расположенной на расстоянии r от центра сферы.
Следовательно, для разности потенциалов будем иметь
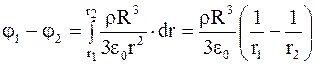 . (1.81)
. (1.81)
Если принять r2 = ¥ и r1 = r , то потенциал поля, порождаемого шаром в точке, на расстоянии r от его центра
 . (1.82)
. (1.82)
Потенциал на поверхности шара (r = R)
 . (1.83)
. (1.83)
Потенциал внутри шара (r<R)
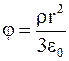 . (1.84)
. (1.84)
Дата добавления: 2016-06-22; просмотров: 4764;











