Поле двух бесконечно протяженных, равномерно заряженных плоскостей

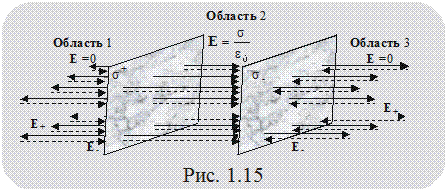
Пусть имеются две бесконечно протяженные, равномерно заряженные плоскости, заряд на которых равномерно распределен с поверхностными плотностями +s и -s (рис. 1.15).

Каждая из плоскостей вокруг себя создаёт электрическое поле с напряженностью соответственно E₊ и E_-. В пространстве, как вне плоскостей, так и между ними, существует в этом случае результирующее электрическое поле с напряженностью

E = E₊ + E_-. (1.63)

Численное значение вектора напряженности электрического поля от одной из плоскостей

.

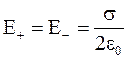В областях 1 и 3 векторы напряженности электрических полей E₊ и E_ равны по величине, но противоположны по направлению. Следовательно, поля компенсируют друг друга, результирующее поле отсутствует, E = 0.

В области 2 векторы напряженности электрических полей E₊ и E_ направлены в одну сторону, результирующее поле характеризуется вектором E, численное значение которого

E = E₊ + E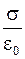_- = . (1.64)

Таким образом, вне объёма, ограниченного плоскостями, поле отсутствует. Поле сосредоточено между плоскостями, и напряженность его одинакова по величине и направлению во всех точках ограниченной области.

Полученный результат оказывается справедливым и для поля плоскостей конечных размеров. Отклонение от полученного результата наблюдается только вблизи краёв (так называемый краевой эффект).

Воспользовавшись соотношением 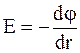можно определить разность потенциалов электрического поля между плоскостями. Имеем

,

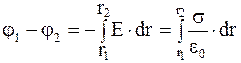где .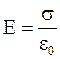

Откуда

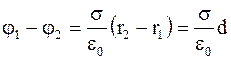, (1.65)

где r₂ - r₁ = d – расстояние между плоскостями.