Поле заряженной сферической поверхности

Дана равномерно заряженная по поверхности сфера, радиус которой R, а поверхностная плотность заряда s.

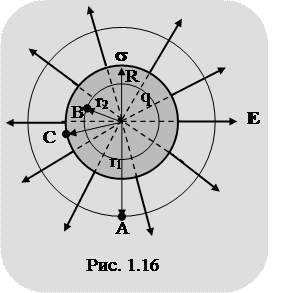Для определения величины напряженности электрического поля в некоторой точке "А", находящейся на расстоянии r₁>R, воспользуемся теоремой Остроградского-Гаусса. С этой целью вокруг заданной сферы построим некоторую замкнутую сферическую поверхность радиусом r₁, равным расстоянию от рассматриваемой точки поля до центра сферы (рис. 1.16).

Линии вектора напряженности электрического поля в этом случае перпендикулярны поверхности заданной сферы, направлены по радиальным прямым.

Поток вектора напряженности электрического поля через построенную поверхность

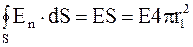. (1.66)

Заряд, находящийся внутри построенной поверхности,

. (1.67)

На основании теоремы Остроградского-Гаусса имеем

.

Откуда напряженность электрического поля в точке "A"

. (1.68)

Из выражения (1.68) можно сделать выводы:

а) в точке "C" (r₁ = R)

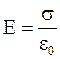; (1.69)

б) в точке "B" (r₁ = r₂<R)

E = 0. (1.70)

Таким образом, внутри сферической поверхности поле отсутствует. Вне сферы на любом расстоянии r от центра сферы

, (1.71)

где , т.е. оно такое же, как и поле точечного заряда, помещенного в центр сферы.

График зависимости напряженности электрического поля от расстояния до центра сферы представлен на рис. 1.17.

Разность потенциалов между двумя точками поля в этом случае

, (1.72)

где - напряженность элект-рического поля в точке на расстоянии r>R от центра сферы.

Таким образом,

. (1.73)

Если принять r₁ = r и r₂ = ¥, то потенциал поля вне сферической поверхности

, (1.74)

что совпадает с соотношением для потенциала поля точечного заряда.

Внутри сферической поверхности потенциал всюду одинаков:

. (1.75)

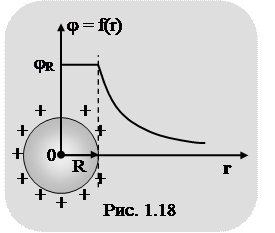
График зависимости потенциала от расстояния до центра сферы (j = f(r)) представлен на рис. 1.18.