Проводники и их классификация

Проводники – вещества, хорошо проводящие электрический ток, т.е. обладающие высокой электропроводностью (небольшим удельным электросопротивлением r ~ 10^-6 ¸ 10^-4 Ом×м).

К проводникам относятся: металлы и их сплавы, графит, некоторые окислы и сернистые соединения металлов, электролиты и плазма.

Носителями зарядов в проводниках являются:

а) в металлах и их сплавах - квазисвободные электроны проводимости;

б) в электролитах - положительные и отрицательные ионы;

в) в плазме - свободные электроны и ионы.

Все проводники можно подразделить на проводники первого и второго рода.

Проводники первого рода - металлы и их сплавы, графит, некоторые окислы и сернистые соединения металлов.

Проводники второго рода - электролиты (растворы солей кислот и щелочей).

Отличительными особенностями проводников первого рода являются:

а) электрический ток в них представляет собой упорядоченное движение квазисвободных электронов проводимости, при этом никаких химических изменений в проводниках не происходит;

б) кристаллическое строение. Это последовательность правильно расположенных групп ионов, образующих пространственную кристаллическую решетку, в межузельном пространстве которой находятся квазисвободные электроны проводимости.

2.2. Электростатическое поле в полости
идеального проводника и у его поверхности.
Электростатическая защита.
Распределение зарядов в объеме проводника
и по его поверхности

В отсутствие внешнего электрического поля заряды узлов кристаллической решетки металлических проводников скомпенсированы зарядами квазисвободных электронов проводимости. В поле на электроны проводимости действуют сила

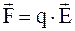. (2.1)

В результате происходит перераспределение электрических зарядов в объёме проводника (электростатическая индукция), которое приводит к появлению внутри проводника "собственного" электрического поля с напряженностью E^', направление которого противоположно направлению вектора напряженности внешнего электрического поля E_o. Поэтому условием перераспределения (движения) электрических зарядов в объёме проводника может служить выражение

E = E_o + E^' ¹ 0, (2.2)

где E – напряженность результирующего электрического поля.

Перераспределение электрических зарядов в объёме проводника (рис. 2.1, а) приводит к искажению внешнего электрического поля (рис. 2.1, б).

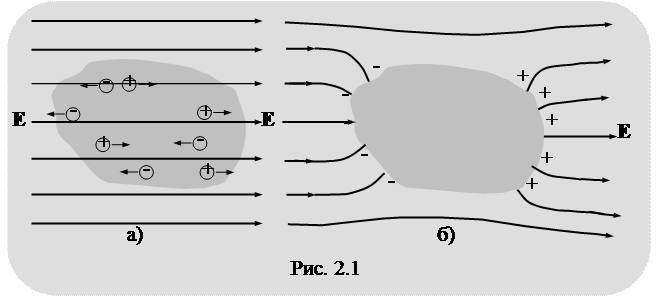
При

E= E_o + E^' = 0 (2.3)

перераспределение электрических зарядов внутри проводника прекращается (рис. 2.1б). Выражение (2.3) называют условием равновесия зарядов в проводнике.

Таким образом, нескомпенсированные электрические заряды (в заряженном проводнике) могут находиться только на его поверхности.

Доказать приведенное утверждение можно, воспользовавшись теоремой Остроградского – Гаусса:

.

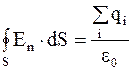Так как внутри проводника E = 0, то E_n = E×cosa = 0, 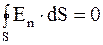. Следовательно,

,

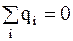что и требовалось доказать.

Между поверхностной плотностью заряда проводника и напряженностью электрического поля вблизи его поверхности существует связь, которую можно установить из следующих рассуждений.

Поток вектора напряженности электрического поля E через замкнутую цилиндрическую поверхность, перпендикулярную некоторой площадке dS поверхности проводника (рис. 2.2),

Ф^'_E = Ф^'_o + Ф^''_o + Ф^'_б + Ф^''_б. (2.4)

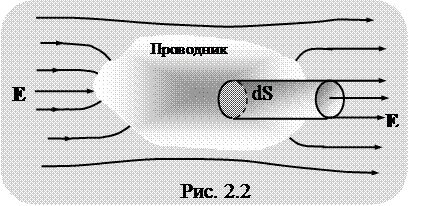Так как внутри проводника электри-ческое поле отсут-ствует (E = 0), то Ф^''_о и Ф^''_б внутри прово-дника равны нулю. Поток вектора нпряженности электрического поля через боковую поверх-ность вне проводника Ф^'_б тоже равен нулю, так как проекция вектора напряженности электрического поля на направление положительной нормали (E_n) в любой точке боковой поверхности равна нулю. Следовательно,

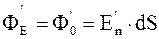. (2.5)

Согласно теореме Остроградского - Гаусса

. (2.6)

В нашем случае можно принять

.

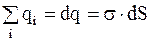Таким образом

,

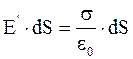а

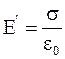. (2.7)

Следовательно, напряженность электрического поля вблизи поверхности проводника пропорциональна поверхностной плотности его заряда.

С этим связан тот факт, что у выпуклых частей проводника напряженность электрического поля и поверхностная плотность электрических зарядов больше, чем у вогнутых (рис. 2. 3). Особенно велики они на остриях. В результате вблизи выпуклых частей проводника возникает ионизация и движение ионов, молекул газа, возникает так называемый "электрический ветер". Заряд проводника при этом уменьшается. Он как бы стекает с поверхности проводника. Такое явление называют истечением заряда с поверхности проводника (с острия).

Поверхностное распределение зарядов на проводниках используется для передачи заряда от одного проводника к другому, в устройстве электростатических машин для получения больших разностей потенциала.

Условие E = 0 внутри проводника используется для устройства электростатической защиты приборов от влияния внешних электрических полей. С этой целью достаточно поместить прибор внутрь проводника – экрана.

Внутри проводника

,

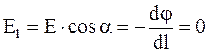что возможно при

E = 0, 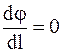, . (2.8)

Таким образом, весь объём проводника, при условии равновесия заряда, является эквипотенциальным.

Поверхность такого проводника также является эквипотенциальной, так как при перемещении по ней в каждой точке вектор напряженности электрического поля E перпендикулярен направлению перемещения (E ^ l), cosa = 0. Следовательно,

; .

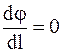Это означает, что при соединении проводников с различными потенциалами происходит выравнивание потенциалов на проводниках за счет переноса зарядов от одних проводников к другим. Это происходит до тех пор, пока у всех проводников потенциал не станет одним и тем же.

Равенство потенциала на всех соединенных между собой проводниках используется для экспериментального определения потенциала в различных точках электрического поля.

2.3. Электроемкость уединенного проводника
и ее физический смысл

Опыты показывают, что изменение заряда проводника приводит к изменению его потенциала, а отношение изменения заряда dq (Dq) к изменению потенциала dj (Dj) для данного проводника остается величиной постоянной. Это отношение и называют электрической емкостью (электроемкостью) уединенного проводника. Следовательно, каждый проводник можно характеризовать электроемкостью (отношением)

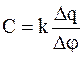или 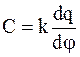, (2.9)

где k - коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин.

В системе СИ k = 1, поэтому

или 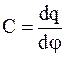. (2.10)

Таким образом, электроемкость уединенного проводника – это физическая величина, численно равная количеству электричества, на которое необходимо изменить заряд проводника, чтобы его потенциал изменился на единицу. В этом и заключается физический смысл электроемкости уединенного проводника.

Так как при q = 0, j = 0, а изменение заряда проводника Dq пропорционально изменению его потенциала Dj, то и заряд проводника q пропорционален его потенциалу j. Следовательно,

. (2.11)

В системе СИ

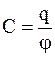. (2.12)

Экспериментальные данные говорят о том, что электроемкость (емкость) проводника зависит только от формы его поверхности, линейных размеров, расположения проводника относительно других проводников и диэлектрической проницаемости среды, окружающей проводник.

За единицу емкости принимается емкость такого проводника, потенциал которого изменяется на единицу при изменении его заряда на единицу.

В системе СИ единицей емкости является Фарада. 1 Ф = 1 Кл/В = = 10^-6 мкФ = 10^-12 пФ.