Поле бесконечно протяженной, однородно заряженной плоскости

Имеется бесконечно протяженная, однородно заряженная плоскость. Заряд на плоскости равномерно распределен с поверхностной плотностью s. Так как заряд равномерно распределен по поверхности плоскости, то поверхностная плотность заряда 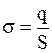. Линии вектора напряженности электрического поля E перпендикулярны плоскости, поле – однородное.

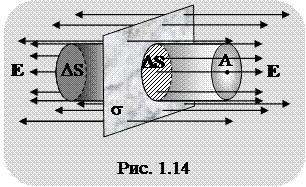Для расчета напряженности электрического поля воспользуемся теоремой Остроградского-Гаусса. С этой целью выделим на плоскости некоторую площадку DS, построим замкнутую цилиндрическую поверхность, образующие которой параллельны линиям вектора E. На одном из оснований этой поверхности находится рассматриваемая точка "А", в которой определяется напряженность электрического поля (рис. 1.14).

Поток вектора напряженности электрического поля через построенную замкнутую цилиндрическую поверхность равен потоку E_б через боковую поверхность и потокам E_о через два основания:

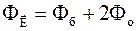. (1.58)

С одной стороны, так как поток вектора Ф_б через боковую поверхность равен нулю (линии вектора E не пересекают боковую поверхность), то полный поток вектора E

, (1.59)

то есть

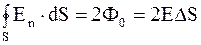, (1.60)

где Ф_o = EDS.

С другой стороны,

,

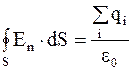где .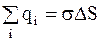

Таким образом, имеем

,

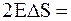
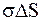а

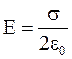. (1.61)

Из полученного результата (1.61) видно, что на любых расстояниях от бесконечно протяженной, равномерно заряженной плоскости напряженность электрического поля не зависит от расстояния и имеет одно и то же направление, что и подтверждает его однородность.

Воспользовавшись соотношением 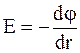можно определить разность потенциалов между двумя точками электрического поля, находящимися на расстояниях r₁и r₂ от плоскости.

Имеем

,

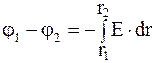где

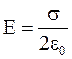
или

.

Откуда

, (1.62)

где r₂ - r₁ = d – расстояние между рассматриваемыми точками.

Из (1.62) видно, что разность потенциалов между двумя точками поля в данном случае не зависит от расположения точек относительно плоскости, а определяется только расстоянием между ними.