Электрическое поле, порождаемое бесконечно длинным, равномерно заряженным стержнем

Характеристикой линейного распределения заряда является линейная плотность заряда. Физическая величина, численно равная заряду, находящемуся на единице длины, 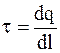. При равномерном распределении заряда .

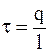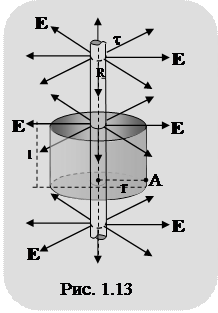Для определения напряженности электрического поля, порождаемого бесконечно длинным, равномерно заряженным стержнем, радиус которого R, воспользуемся теоремой Остроградского-Гаусса.

Для чего вокруг стержня проведем замкнутую (в рассматриваемом случае цилиндрическую) поверхность конечной длины, на боковой поверхности которой находится точка "А". Линии вектора E перпендикулярны оси стержня и боковой поверхности цилиндра (рис. 1.13).

Поток вектора напряженности электрического поля через построенную замкнутую цилиндрическую поверхность

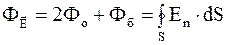, (1.54)

где Ф_o = 0, т.к. E_n = E×cosa = 0.

Следовательно

. (1.55)

На основании теоремы Остроградского-Гаусса

,

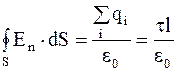тогда

= ,

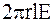а

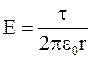. (1.56)

Формула (1.56) справедлива не только для электрического поля заряженного стержня, но и для полей заряженных проводников, цилиндров, 2-х коаксиальных цилиндрических поверхностей, заряженных с одинаковой по величине линейной плотностью заряда t.

Для того чтобы определить разность потенциалов между двумя любыми точками такого поля, необходимо воспользоваться соотношением 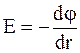, откуда

.

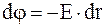Следовательно

,

а

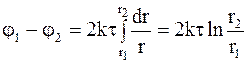, (1.57)

где r₁ и r₂ – соответственно расстояние от оси стержня (цилиндра) до рассматриваемых точек электрического поля.