Оценка энергии образования точечных дефектов
Для оценки ΔE и ΔEш прежде всего было рассчитано изменение кулоновской энергии при образовании точечных дефектов и взаимодействие смещенногоиона совсеми остальными, которые считались неподвижными. Определенное таким способом значение ΔE и ΔEш оказались слишком большими. Например, для иона Ag+ в кристаллах AgBr, изменениеэнергии Маделунга при образовании дефектов по Френкелю ΔEф составляет 10 эВ. В действительности, значение ΔEф не должно превышать значения энергии активации удельной проводимости,т.е. 1 ÷ 2 эВ.
Следовательно, необходимо учитывать какие-то факторы. Такими факторами могут быть:
а) смещение ионов, окружающих дефект.
б) деформация электронных оболочек атомов
Расчет энергии ΔE и Eшпредложен Н. Моттом. Поляризационная поправка была получена им с учетом энергии взаимодействия точечных ионов решетки с дефектом. В этом случае потенциал электрического поля в центре дефекта φ находилисуммированием полей точечных диполей, представляющих собой поляризованные атомы кристалла.
Для бинарных дефектов потенциал электрического поля рассчитывали по формуле:
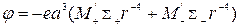 , ()
, ()
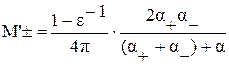 , ()
, ()
где α – ионная поляризуемость, которую можно найти по соотношению Клаузиуса-Мосотти, а значение решеточных сумм 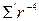 ,из таблиц для решеток данного типа. Подставляя численные значения, можно получить:
,из таблиц для решеток данного типа. Подставляя численные значения, можно получить:
| Потенциал поля | NaCl | KBr |
| φр (к) | 6,04 | 5,03 |
| φра (а) | 5,02 | 4,58 |
Энергия образования парного дефекта по Шоттки складывается из энергий, необходимых для удаления положительного и отрицательного иона из решетки в бесконечность (Ep+(o); Ep-(o)) и энергии, которая выделяется при перемещении этих ионов на поверхность кристалла (EpL+) ; (EpL-):
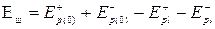 , ()
, ()
Результаты вычислений энергии образования дефектов для NaCl, KCl и KBr приведены в таблице :
Таблица
Энергии образования парных дефектов по Шоттки для кристаллов NaCl, KCl и KBr полученных экспериментально и рассчитанных теоретически
| Энергия, эВ | NaCl | KCl | KBr |
| Ep+(o) | 4,62 | 4,47 | 4,23 |
| Ep-(o) | 5,18 | 4,79 | 4,60 |
| EpL+ + EpL- | 7,94 | 7,18 | 6,91 |
| Ep, теор. | 1,86 | 2,08 \ | 1,92 |
| Ep, экспер. | 1,82 | 2,03 | 1,90 |
Аналогичным образом могут быть рассчитана энергия образования точечных дефектов по Френкелю ΔE.
В теории Мотта не учитывалось взаимодействие дефектов между собой. Предполагалось, что они ведут себя подобно частицам идеального раствора.
Учитывая, что вакансии и междоузельные ионы заряжены, можно ожидать, что они будут взаимодействовать между собой, как ионы в растворах электролитов. Такое взаимодействие, при не слишком больших концентрациях удовлетворительно описывается теорией Дебая-Хюккеля. В теории Дебая-Хюккелядля твердых тел по аналогии с растворами вводится коэффициент активности ионов (f)
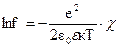 ,
,
где 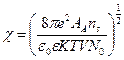
где f- активность ионов, e – заряд иона (вакансия); ε – диэлектрическая проницаемость; 
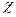 - обратный Дебаевскийрадиус;
- обратный Дебаевскийрадиус; 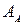 – число Авогадро; n – равновесная концентрация вакансий.
– число Авогадро; n – равновесная концентрация вакансий.
С учетом взаимодействия дефектов формула для расчета равновесной концентрации точечных дефектов по Шоттки будет:
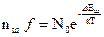 , ()
, ()
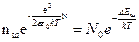 , ()
, ()
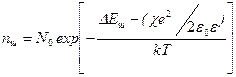
Поскольку Дебаевский радиус 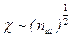 – то энергия образования дефектов прогрессивноснижается с ростом концентрации дефектов, этов принципе может привести к катастрофическому увеличению их количества при достижения критической температуры.
– то энергия образования дефектов прогрессивноснижается с ростом концентрации дефектов, этов принципе может привести к катастрофическому увеличению их количества при достижения критической температуры.
Модель Дебая-Хюккелядает адекватную картину взаимодействия дефектов решетки лишьдо тех пор, пока они достаточно удалены друг от друга. Это происходит потому, что при малых расстояниях между дефектами, сравнимых с параметрамирешетки, становится непригодным представление дефекта в виде точечного или сферического заряда в диэлектрическом континууме. Иными словами, при сближении дефектов разного знака происходит их ассоциация.
В случае дефекта Френкеля, т.е. пары междоузельный ион- вакансия, такая ассоциация, вероятно должнапривести к исчезновению дефекта. Однако, при сближении разноименных вакансий или междоузельных атомов возникает комбинированный дефект, суммарный заряд которого равен нулю,нокоторый обладает некоторым дипольным моментом. Такие двойные дефекты могут перемещаться по решетке, как и простые дефекты.
Законы случайных блужданий и диффузия в кристаллах.
Вакансии и междоузельные ионы не остаются закрепленными в определенных местах кристаллической решетки, а непрерывно блуждают по всему объему кристалла, скачками переходя с занимаемых ими мест на соседние. Эти перемещения дефектов аналогичны хаотическому блужданию молекул газа с той лишь разницей, что они происходят путем скачков строго определенной длины, равной расстоянию между соседними эквивалентными позициями, а направления скачков строго фиксированы и зависят от структуры решетки. Блуждания дефектов в кристаллической решетке можно рассматривать случайными в том смысле, что направления двух последовательных скачков данной частицы или квазичастицы взаимнонезависимы.
Подобные движения могут быть описаны на основе теории вероятностей. Если мы будем следить за каким-то избранным дефектом в течение достаточно большого времени t, то среднее смещение 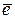 по прошествии времени t должно быть равно 0
по прошествии времени t должно быть равно 0 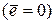 .
.
В основе теории диффузии лежит фундаментальное уравнение, связывающее среднеквадратичное смещение 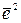 хаотически движущейся частицы со временем ее движения.
хаотически движущейся частицы со временем ее движения.
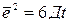 , где Д- коэффициент диффузии.
, где Д- коэффициент диффузии.
Это уравнение справедливо применительно к любой изотропной среде беспорядочно движущихся частиц (броуновское движение).
Для решеток не кубических, можно использовать аналогичное уравнение, однако с другим численным коэффициентом. Если частица совершила большое число (n) последовательных скачков, длина которых одинакова и равна r, то средний квадрат смещения частицы в общем случае равен:
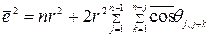 , где
, где 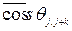 - среднее значение косинуса угла между направлениями j-го и (j+k)- го скачка. Когда скачки совершенно случайны и направления последующего скачка не зависит от направления предыдущего, среднее значение
- среднее значение косинуса угла между направлениями j-го и (j+k)- го скачка. Когда скачки совершенно случайны и направления последующего скачка не зависит от направления предыдущего, среднее значение 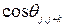 должно равняться нулю и
должно равняться нулю и 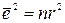 .
.
Поскольку n есть число перескоков за длительное время t, то, обозначая среднее время между двумя перескоками через 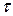 , получим:
, получим:
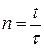 и
и 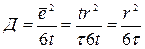
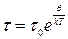
Использование уравнения требует применение конкретной модели.
Чтобы проиллюстрировать схему расчета, рассмотрим самодиффузию катионов в решетке NaCl, идущую путем перемещения вакансий.
Механизм диффузии.
Частица колеблется у своего положения равновесия с частотой 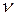 в течении некоторого времени
в течении некоторого времени 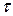 . Затем, благодаря взаимодействию с окружающими ионами, частица приобретает энергию U, которой оказывается достаточно, чтобы перескочить барьер, разделяющий два соседних положения равновесия (узел и вакансию). К моменту окончания скачка, частица теряет часть своей энергии, отдавая ее окружающим ионам и задерживается в новой позиции. Через некоторое время в образовавшуюся вакансию перемещается другая частица. Время оседлой жизни частицы должно быть обратно пропорционально по количеству вакансий, находящихся в ее ближайшем окружении. Для катионной подрешетки NaCl число ближайших соседей одного знака равно 12. Относительная доля вакансий
. Затем, благодаря взаимодействию с окружающими ионами, частица приобретает энергию U, которой оказывается достаточно, чтобы перескочить барьер, разделяющий два соседних положения равновесия (узел и вакансию). К моменту окончания скачка, частица теряет часть своей энергии, отдавая ее окружающим ионам и задерживается в новой позиции. Через некоторое время в образовавшуюся вакансию перемещается другая частица. Время оседлой жизни частицы должно быть обратно пропорционально по количеству вакансий, находящихся в ее ближайшем окружении. Для катионной подрешетки NaCl число ближайших соседей одного знака равно 12. Относительная доля вакансий 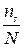 , то
, то 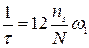 , где
, где 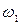 - вероятность того, что в единицу времени катионная вакансия перескочит из одного узла в другой.
- вероятность того, что в единицу времени катионная вакансия перескочит из одного узла в другой.
Расстояние между ближайшими соседями равно: 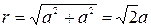 , где а- расстояние между катионами и анионами. Тогда
, где а- расстояние между катионами и анионами. Тогда 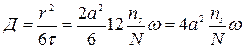 ,
, 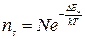 ,
, 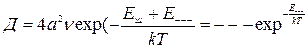 Формула ??????
Формула ??????
Вероятность должна быть пропорциональна частоте колебаний 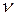 и величине
и величине 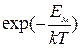
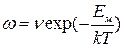
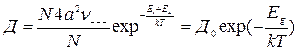
При наличии бивакансий коэффициент диффузии :

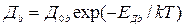
Методика измерения диффузии в кристаллах.
Определение коэффициента диффузии в ионных кристаллах может быть осуществлено с помощью радиоактивных изотопов – это один из прямых и надежных методов.
Наибольшее распространение получил метод секционирования (метод снятия слоев). В основе метода лежат следующие соображения. Если на торец исследуемого образца, изготовленного в виде цилиндра или параллепипеда, нанести очень тонкий слой той же соли, содержащей радиоактивный изотоп, то с течением времени радиоактивность будет распространяться в глубь образца вследствие диффузии.
Рисунок 5.
Предполагая, что толщина образца достаточно велика. Можно использовать для описания диффузии решение уравнения Фика:
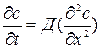 , где с- концентрация.
, где с- концентрация.
Решение этого уравнения:
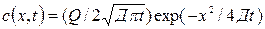 , где Q – количество вещества, приходящееся на 1 см2 площади образца в начальном слое; х – расстояние от начального слоя; t- время. Поскольку радиоактивность
, где Q – количество вещества, приходящееся на 1 см2 площади образца в начальном слое; х – расстояние от начального слоя; t- время. Поскольку радиоактивность 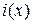 пропорциональна концентрации диффундирующего изотопа, то
пропорциональна концентрации диффундирующего изотопа, то 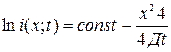
Практически измерения проводятся следующим образом:
1. Нанесение радиоактивного слоя
2. Проведение диффузионного отжига при постоянной температуре в течение времени t.
3. Последовательное снятие слоев с образца и измерение его радиоактивности.
Наносят радиоактивный изотоп несколькими способами:
1. Вакуумного напыления.
2. Наносят суспензию, потом испаряют.
3. Изотопный обмен в растворе поверхности образца.
Рисунок 6.
Требования, которые предъявляют к слою активного вещества, сводятся к двум моментам. Первый - необходим хороший контакт по всей поверхности. Второе – Начальная толщина слоя должна быть как можно меньше. Несоблюдение этих требований ведет к отклонению графики от прямой.
Диффузионный отжиг проводится при постоянной температуре от нескольких часов до нескольких суток. Если время отжига не столь длительное, большая ошибка вносится тем, что нагрев и охлаждение образца осуществляется не мгновенно. Поэтому сокращение времени отжига нежелательно.
Слои, как правило, ----- микротоком, который позволяет нарезать параллельные торцу образца слои толщиной до 10 мкм, или растворяют в ----растворе.
Концентрация носителей определена нами ранее, необходимо определить подвижность носителей.
При наложениипостоянного внешнего поля характер потенциальной кривой изменяется. Если поле однородно, то потенциальная энергия иона в этом поле должна изменяться с координатой линейно. Графически это можно представить как сумму линейной части изменения потенциальной энергии и периодического потенциала.
Изображенное изменение потенциальной кривой соответствует положительному иону
При наличии E потенциальная энергия изменяется на qEx
Рисунок 7.
Рисунок 8.
В направлении поля потенциальный барьер уменьшается на величину qEa/2, а в направлении противоположном полю увеличивается на ту же величину. Следовательно, перенос катионов по направлению поля облегчается, против направления поля затрудняется.
Поскольку при расчете подвижности ставили задачу описать движение междоузельных ионов, то следует учесть только междоузлия. Рассмотрим потенциальный рельеф только для междоузельных ионов в виде аналогичнойсхемы и не будем учитывать глубокие потенциальные ямы – узлы. Соответственно глубина каждой ямы будет W. В электрическом поле междоузлия, расположенные на расстоянии «а», смещаются по вертикали на величину 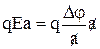 . Следовательно, по отношению к положению, когда E=0 первый минимум поднимается на величину qEa/2, а второй опускается на такую же величину qEa/2.
. Следовательно, по отношению к положению, когда E=0 первый минимум поднимается на величину qEa/2, а второй опускается на такую же величину qEa/2.
Если частота тепловых колебаний ионов в междоузлии ν0, то в отсутствии внешнего электрического поля число перескоков, происходящих в результате теплового движения, в соседние междоузлия 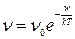 , где ν0 – можно рассматривать как частоту попыток иона «выпрыгнуть» из потенциальной ямы междоузлия, а экспонента характеризует вероятность преодоления барьера с энергией W за счет тепловой энергии kT. Произведение этих величин и дает число фактических перескоков по всем направлениям .
, где ν0 – можно рассматривать как частоту попыток иона «выпрыгнуть» из потенциальной ямы междоузлия, а экспонента характеризует вероятность преодоления барьера с энергией W за счет тепловой энергии kT. Произведение этих величин и дает число фактических перескоков по всем направлениям .
Для заданного направления частота перескоков ν` составляет величину, равную 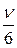 ;
; 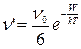
Соответственно частота перескоков катионов по полю: 
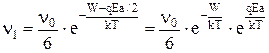
и против поля:
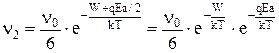
Полагая, что напряженность поля небольшая, так, что qEa << 2kT, раскладываем ?в ряд и ограничимся двумя первыми членами:
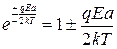
Скорость дрейфа (скорость перемещения катиона по полю) равна разности числа перескоков ν1 и ν2, умноженной на расстояние, проходимое при одном перескоке «a». Действительно, скорость дрейфа можно представить как разность скоростей вдоль и против поля.
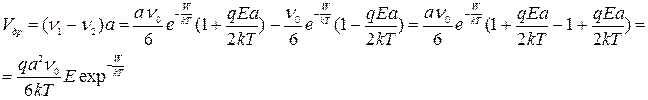 Отсюда подвижность определяется как:
Отсюда подвижность определяется как:
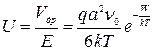
Формулу для подвижности междоузельных ионов можно использовать при расчетах электропроводности, обусловленных дефектами по Френкелю.
Так для монокристаллов, имеющих дефекты по Френкелю, имеем 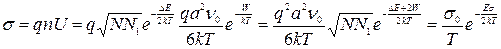
Аналогичным образом можно выразить подвижность и электропроводность для дефектов по Шоттки.
Рисунок 9.
Очевидно, что экспериментально можно определить лишь суммарную величину 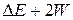
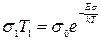
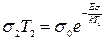
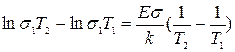
Задание:
Вывести формулу для электропроводности по Шоттки и рассчитать величину электро---- при комнатной температуре t=25о, считая, что W=0,51 эВ и 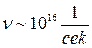 .
.
Уравнения переноса ионов.
Для описания явлений переноса в ионных проводниках вводят понятия тока диффузии и тока дрейфа (миграции).
Под током диффузии jд понимают движение ионов под действием градиента химического потенциала.
Разность концентраций обуславливает перемещение ионов из области с большей концентрацией в область с меньшей концентрацией.
Движение частиц в концентрационных полях описывается двумя уравнениями диффузии, называемыми законами Фика.
I закон Фика выражает обычно, наблюдаемую на опыте, пропорциональность между плотностью потока и градиентом концентрации.
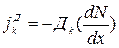 , где N- концентрация k- частиц; Дk – коэффициент диффузии.
, где N- концентрация k- частиц; Дk – коэффициент диффузии.
Для зар--- 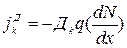
II закон Фика описывает зависимость концентрации от времени.
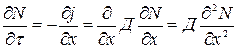
Считается, что коэффициент диффузии не зависит от концентрации и, следовательно от коор-----.
Поток заряженных частиц под действием градиента электрического потенциала создает ток дрейфа jм (миграции), который может быть вычислен:
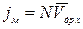
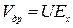
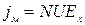 , где jм- плотность тока миграции; N- концентрация частиц;
, где jм- плотность тока миграции; N- концентрация частиц; 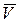 - дрейфовая скорость; U – подвижность.
- дрейфовая скорость; U – подвижность.
Соотношение Нернста- Эйнштейна
Наличие дефектов определяет способность ионных кристаллов проводить электрический ток. Очевидно, должна существовать связь между коэффициентом диффузии ионов (Д) и их подвижностью в электрическом поле (U). Эта связь устанавливается соотношением Нернста- Эйнштейна.
В общем случае ион движется как под действием градиента химического потенциала, так и под действием градиента электрического потенциала.
Если ионы в твердом теле находятся в состоянии равновесия, т.е. потоки диффузии и миграции друг друга компенсируют так, что не возникает суммарного потока, то можно записать:
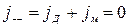
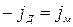 ;
; 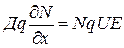 ;
;
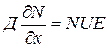
В состоянии равновесия зависимость концентрации частиц от электрического потенциала 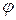 описывается уравнением Максвелла- Больцмана:
описывается уравнением Максвелла- Больцмана: 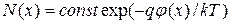 , где
, где 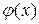 - потенциал, создаваемый полем в точке
- потенциал, создаваемый полем в точке 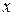 .
.
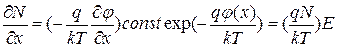
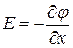
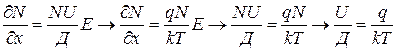
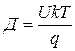
Используя соотношение Нернста-Эйнштейна и выражение для удельной электропроводности можно получить св---- 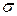 и ---
и ---
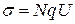
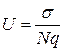
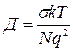
Уравнение Нернста- Эйнштейна в этом случае приводит к простому соотношению между коэффициентом диффузии и проводимостью кристалла. В частности, оказываются равными энергии активации диффузии и проводимости.
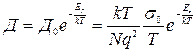
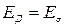
Экспериментальная проверка соотношения Нернста- Эйнштейна для кристаллов показывает, что при соблюдении равенства энергий активации проводимости и диффузии, как правило, 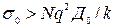
Чтобы объяснить отклонение предэкспоненциального множителя от величины, вычисляемой по уравнению Нернста- Эйнштейна, Бардин и Херинг предложили теорию корреляции.
Сущность этой теории состоит в следующем. Для измерения коэффициентов самодиффузии используются радиоактивные индикаторы. Движение ионов индикаторов в кристаллической решетке формально рассматривается как отвечающее принципу случайных блужданий. На самом деле положение оказывается более сложным. Например, при вакансионном механизме диффузии ион- индикатор не может начать движение до тех пор, пока к нему не подойдет вакансия. Поскольку вероятность подхода вакансий с любой стороны одинакова, направление первого скачка иона- индикатора действительно будет случайным. Однако ситуация становится иной, когда речь идет о вероятности второго и последующих скачков. В самом деле, после первого скачка по соседству с ионом уже имеется одна вакансия. Вероятность того что к нему подойдет еще одна вакансия и он обменяется с ней местом, меньше, чем вероятность обратного обмена с первой вакансией.
Таким образом, направления последующих перемещений индикатора не являются независимыми – между ними существует корреляция. Это приводит к тому, что коэффициент диффузии радиоактивного индикатора Динд отличается от коэффициента диффузии, вычисляемого по уравнению Нернста- Эйнштейна, т.е. ------------ электропро----, поскольку ионы, принимающие участие в электропроводности неотличимы друг от друга и корреляция при их движении отсутствует.
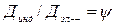 - коэффициент корреляции.
- коэффициент корреляции.
Этот коэффициент зависит от типа кристаллической решетки:
Кубическая объемноцентрированная 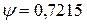
Кубическая гранецентрированная 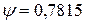
Гексагональная 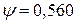
При движении ионов по междоузлиям в связи с тем, что число междоузлий превышает число ионов корреляция отсутствует: 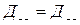
В случае непрямого междоузельного механизма, когда междоузельные ионы движутся, обмениваясь местами с ионами в нормальных узлах решетки, 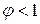 .
.
Строение и свойства твердых электролитов.
Как мы уже говорили, в чистых соединениях дефекты имеют термическую природу и обусловлены разупорядоченностью собственной кристаллической решетки. В примесных соединениях существование точечных дефектов обусловлено необходимостью компенсации избыточного заряда иновалентных примесей. При этом, концентрация дефектов определяется содержанием примеси и, следовательно, может контролироваться в довольно широких пределах, что дает возможность управлять свойствами примесных твердых электролитов.
Наибольший интерес сейчас представляют твердые электролиты, обладающие очень высокой степенью разупорядоченности одной из подрешеток, чаще всего катионной. Общей отличительной чертой электролитов этого класса является наличие в катионной подрешетке большого числа разрешенных мест, существенно превышающего число имеющихся катионов. Поэтому катионы в таких соединениях статистически распределены по всей совокупности разрешенных мест, образуя некоторое подобие катионной жидкости, в которую погружена жесткая ---- подрешетка. В таких системах перенос осуществляется не точечным дефектом, а всей совокупностью катионов.В отличие от кристаллов с точечным дефектом в таких соединениях разупорядоченность охватывает всю структуру в целом. ------------
Принято кристаллические твердые электролиты по своей дефектной структуре делить на три класса:
1. Твердые электролиты с собственной разупорядоченностью
2. Твердые электролиты с примесной разупорядоченностью
3. Твердые электролиты со структурной разупорядоченностью.
Механизм проводимости в твердых электролитах с собственной разупорядоченностью обусловлен образованием дефектов по Шотттки и Френкелю.
Такие ионные проводники обладают низкой проводимостью и большой энергией активации. Имеют структуру типа NaCl и флюорита CaF2.
KF~2,64 эВ, RbCl~2,0 эВ, CaF2~2,2 эВ
Примесная разупорядоченность возникает в ионных кристаллах при легировании их ионами с валентностью, отличной от валентности основного иона. В большинстве случаев образование твердых растворов происходит по типу замещения, когда примесный ион располагается в узле решетки основного соединения. Условия сохранения элек----- приводят к тому, что в решетке образуется вакансия.
Типичный пример КСl, лигированный ионами кальция. Введение двухвалентного иона Са создает вакансию с зарядом ~1+. При этом экспериментально показано, что плотность такого соединения уменьшается.
Общая черта при структурной разупорядоченности – избыток кристаллографических позиций, в которых могут находиться подвижные ионы. Число разрешенных позиций в несколько раз превосходит число соответствующих ионов, что обеспечивает относительную свободу их передвижения, и, следовательно, высокую проводимость.
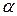 - иодида серебра, слоистые и ка--- структуры?????????
- иодида серебра, слоистые и ка--- структуры?????????
Структуры ионных соединений.
Представлениям о регулярных плотноупакованных ионных решетках ближе всего сответствуют кристаллы галогенидов щелочных металлов, поскольку составляющие их ионы имеют замкнутую электронную оболочку инертного газа и могут в первом приближении рассматриваться как заряженные твердые шарики. При образовании решеток из таких ионов выполняется принцип максимальной координации, т.е. каждый ион стремится окружить себя максимальным числом соседей. Если бы ионы не были заряжены и имели одинаковые диаметры, то это максимальное координационное число определялось бы чисто геометрически. Поскольку ионы заряжены, приходиться учитывать такое требование, как электронейтральность решетки. Максимальное координационное число в ионных решетках равно 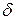 . Из-за различия в размерах ионов координационное число может быть меньше.
. Из-за различия в размерах ионов координационное число может быть меньше.
Из жестких сферических ионов можно построить три кубические плотноупакованные решетки. Эти решетки соответствуют трем реальным кристаллическим структурам, образуемым одноатомными катионами и анионами (М+, Х- или М2+, Х2-: в к--- элементов Cs Cl, NaCl, ZnS).
В решетке CsCl каждый ион окружен ионами противоположного знака, располагающимися по вершинам куба, т.е. реализуется максимальное координационное число. Ионы Cs+ и Cl- образуют простые кубические решетки, как бы --- ставленные одна в другую.
Решетка NaCl состоит из сочетания двух кубических гранецентрированных подрешеток – катионной и анионной. Каждый ион окружен шестью ионами противоположного знака, которые располагаются по вершинам октаэдра.
В структуре сфалерита (цинковой обманки ZnS) катионы Zn2+ и анионы S2- образуют гранецентрированные кубические решетки, вставленные в друг друга, так что каждый ион имеет четырех соседей противоположного знака, расположенных по вершинам тетраэдра.
Вид решетки в значительной степени зависит от соотношения радиусов ионов. Если соотношения радиусов катионов и анионов близки, образуется решетка CsCl с максимальной координацией. В этой решетке кристаллизуются также CsBr, CsI.
Если радиус атома существенно превышает радиус катиона, решетка CsCl становится неустойчива, потому что -----, образуемая плотноупакованными атомами, слишком велика для катиона. В этом случае образуется решетка NaCl, характерная для большинства галогенидов щелочных металлов. При еще большем различии радиусов она также становится нестабильной и переходит в решетку сфалерита.
Считается, что СsСl устойчива до отношения r-/r+ 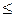 1,37; решетка NaCl в интервале 1,37
1,37; решетка NaCl в интервале 1,37 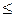 r-/r+
r-/r+ 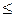 2,44; решетка сфалерита при r-/r+
2,44; решетка сфалерита при r-/r+ 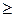 2,44.
2,44.
Однако, наряду с плотными ионными решетками, реальные кристаллы могут образовывать дефектные структуры. Существует две принципиальные возможности возникновения дефектных структур:
1. Беспорядочное статистическое распределение двух разных типов ионов по эквивалентным узлам решетки – дефектные структуры с завершенной решеткой.
2. Частичное заполнение узлов решетки – дефектные структуры с незавершенными решетками.
Вакантные узлы в дефектных структурах могут быть распределены в определенном порядке или статистически пере----- с занат---- - именно такие разупорядоченные структуры проявляют высокую ионную проводимость.
Иодистое серебро AgI.
Низкотемпературные фазы иодистого серебра 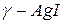 и
и 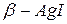 имеют сравнительно низкую проводимость при комнатных температурах ~ 10-5 1/Ом – и при температуре 1470С переходят в
имеют сравнительно низкую проводимость при комнатных температурах ~ 10-5 1/Ом – и при температуре 1470С переходят в 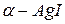 , которая сохраняется вплоть до температуры плавления 5550С и является суперионным проводником. Решетка
, которая сохраняется вплоть до температуры плавления 5550С и является суперионным проводником. Решетка 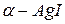 образована плотной объемноцентрированной упаковкой ионов
образована плотной объемноцентрированной упаковкой ионов 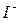 . Элементарная ячейка включает 2 иона
. Элементарная ячейка включает 2 иона 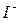 (центральный ион
(центральный ион 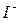 и по
и по 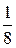 от каждого из 8 ионов в вершинах куба и соответственно 2 иона
от каждого из 8 ионов в вершинах куба и соответственно 2 иона 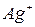 ). Однако ионы
). Однако ионы 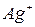 не занимают определенных мест, а распределяются статистически по 42 позициям трех размерных типов. При наличии столь большого числа эквивалентных мест катионы вряд ли могут рассматриваться как жестко закрепленные в тех или иных положениях. С учетом их высокой подвижности представляется вероятным, что они непрерывно кочуют по доступным позициям аналогично частицам жидкости или газа. Таким образом,
не занимают определенных мест, а распределяются статистически по 42 позициям трех размерных типов. При наличии столь большого числа эквивалентных мест катионы вряд ли могут рассматриваться как жестко закрепленные в тех или иных положениях. С учетом их высокой подвижности представляется вероятным, что они непрерывно кочуют по доступным позициям аналогично частицам жидкости или газа. Таким образом, 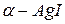 являет собой типичный пример твердого электролита, содержащего анионную кристаллическую решетку и катионную квазижидкость.
являет собой типичный пример твердого электролита, содержащего анионную кристаллическую решетку и катионную квазижидкость.
Соединения меди.
Ионы одновалентной меди сходны с ионами серебра и поэтому следует ожидать, что соединения Cu(I) также будут образовывать высокопроводящие фазы. Это действительно имеет место для галогенидов меди CuI и CuBr, структура 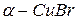 (4700) близка к структуре
(4700) близка к структуре 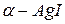 и является разупорядоченной.
и является разупорядоченной.
Полиалюминаты.
Твердыми электролитами являются полиалюминаты одновалентных металлов M2O×nAl2O3, где n=5¸11, а М- Li,Na,K,Rb,Cs,Ag ?????- 
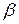 глиноземы.
глиноземы.
Строение – плоские блоки, образованные атомами кислорода и алюминия. В каждом блоке атомы кислорода образуют плотнейшую кубическую упаковку. В октаэдрических и тетраэдрических пустотах рас---- атомы алюминия. Они ------ «с---« атом—кислорода. В щелях находятся атомы та---.
Особенности движения ионов проводимости в твердых электролитах.
Теория транспорта ионов в твердых электролитах до сих пор не создана. Экспериментально наблюдается отклонение от соотношения Нернста-Эйнштейна т.е. количественное сопоставление проводимости и диффузии приводит к несовпадению в 2-3 раза.
Модель кооперативного движения.
В ряде работ было высказано предположение, что наблюдаемые отклонения могут быть обусловлены кооперативностью движения ионов проводимости в решетке твердого электролита. Простейшая модель такого типа была предложена Йокотой.
Рассмотрим линейную цепочку из (n+1) катионных узлов решетки.
Рисунок.
Пусть узел, обозначенный через 0, занят меченым ионом А0, узлы от 1 до (n-1) – обычными ионами, а узел n – вакантный. Поскольку энергия активации миграции в твердых электролитах мала, ион А0 может переместиться в узел 1, выбив из него ион А1. Тот переместится в положение 2 и т.д., пока ион Аn-1 не перейдет в вакантный узел. При этом произойдет n скачков в одном направлении, т.е. вкладов в перенос тока, но лишь один вклад в диффузию радиоактивного изотопа.
На основе этих предположений рассчитываем коэффициенты корреляции: 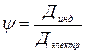 ?????
?????
Дата добавления: 2016-06-22; просмотров: 2499;











