Модель газоподобных ионов.

Была сделана попытка использования для описания переноса в твердых электролитах модель, в которой подвижным ионам приписываются некоторые свойства газовых молекул.

В основе модели лежит представление трансляционного движения термически возбужденного иона между двумя локализованными состояниями как движение газообразной частицы массой М, перемещающейся через решетку «свободным» образом со скоростью V и энергией 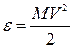. Энергетический спектр этих возбужденных частиц предполагается непрерывным для всех энергий, удовлетворяющих условию 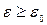и исчезает при 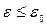. Величину 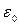можно рассматривать как энергию связи иона проводимости в локализованном состоянии.

Таким образом, --- лируется два состояния ионов проводимости: локализованное ( 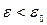) и возбужденное ( 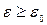). Возбужденный ион в процессе движения взаимодействует с жесткой частью кристаллической решетки, тормозится и вновь переходит в локализованное состояние. Поэтому можно ввести в качестве характеристики движения время жизни возбужденных ионов 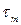и среднюю длину свободного пробега .

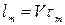Рассматриваемая модель аналогична модели Друде и Лоренца.

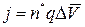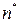Плотность тока под действием поля Е , где - концентрация возбужденных ионов, 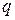- заряд иона проводимости, 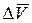- средняя скорость упорядоченного движения заряженных частиц под действием поля.

За время свободного пробега 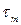ион испытывает действие силы qE, сообщающей ему постоянное ускорение 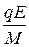. К концу свободного пробега скорость в направлении поля достигает значения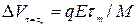

Поскольку в локализованном состоянии скорость равна нулю, то средняя скорость возбужденного иона за период 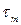составляет:

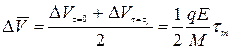
Скорость дрейфа мала по сравнению с тепловым движением V. Поэтому время свободного пробега не должно зависеть от наличия поля и всегда равно .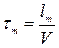

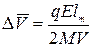, тогда 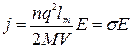, где

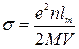
Концентрация свободных ионов согласно формуле Больцмана может быть записана: 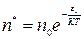, где n₀- общая концентрация ионов проводимости.

Средняя кинетическая энергия ионов проводимости равна:

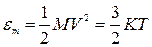
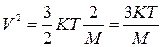
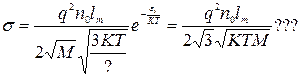
Пример:

n-1,57×10²² 1/см³; e~0,1 эВ; =2,2 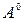; 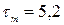×10^-13 сек –близко к ????

Не все хорошо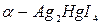

Модель трансляционных скачков.

Более традиционная модель транспорта - модель трансляционных скачков.

Различие этой модели от модели тр??? ионных ???? обусловлена высокой концентрацией подвижных носителей заряда и низкой энергией активации миграции ионов. Армстронг????

Рисунок 10.

Пусть решетка твердого электролита содержит два типа мест (1 и 2), доступных для катионов проводимости. Возможны четыре вида элементарных скачка.

Рисунок.

со скоростью V₁₁ и энергией g₁

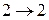cо скоростью V₂₂ и энергией g₂

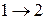cо скоростью V₁₂ и энергией g₁

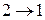со скоростью V₂₁ и энергией g₂

Найдем выражение для 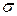в этом случае: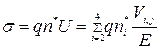

Концентрация:

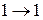
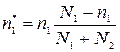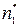, где - концентрация способных к перемещению????? катионов; 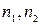- равновесные концентрации ионов в узлах 1 и 2; 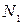и 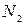- число узлов решетки сортов 1 и 2.

; ;

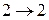
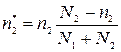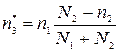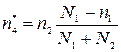
Определим скорость V_ij:

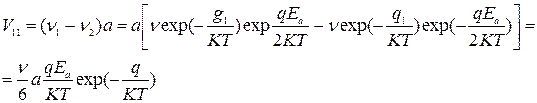
По полю: 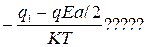Против поля: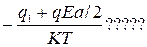

Предположим, что 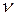- эффективная частота колебаний ионов в узлах 1 и 2 одинакова.

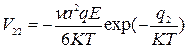
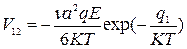
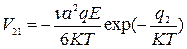
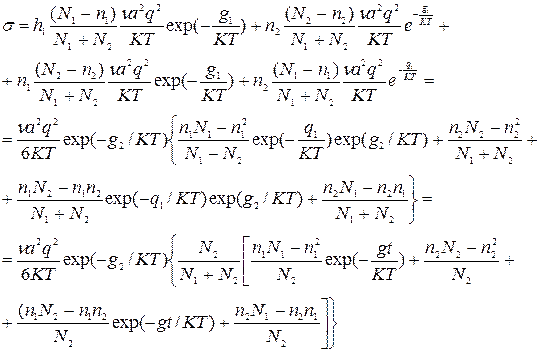
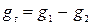
Предположим, что общее число ионов проводимости 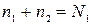равно числу узлов типа 1. Такое предположение оправдано, если считать места типа 1 нормальными узлами решетки, а места 2 – междоузельными.

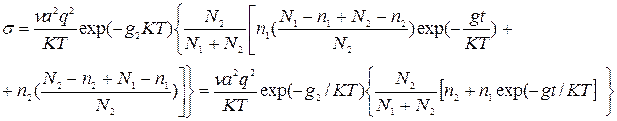При этом выражении в квадратных скобках можно рассматривать как концентрацию возбужденных ионов проводимости, способных к перемещению.

Если g₁>>g₂ или свободная энергия активации скачка иона из узла 1 существенно превышает свободную энергию скачка из узла 2, второй член в скобках становится м---, g_t – большое.

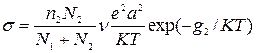
При g_t=0, что соответствует полной разупорядоченности g₁=g₂. Нет различий между узлами и междоузлиями.