Дефекты по Френкелю.

Согласно теории Френкеля при любой конечной температуре в кристалле должны существовать точечные дефекты решетки, обусловленные тепловыми флуктуациями.

Дефект по Френкелю состоит из пустого узла кристаллической решетки и атома в междоузлии. Как правило, в междоузлии оказывается ион, а не нейтральный атом. Соответственно вакансия в узле имеет заряд противоположного знака (рис.)

При переходе иона из узла в междоузлие, его энергия возрастает на величину Δ E, которую называют энергией диссоциации – та же величина представляет собой энергию образования дефекта по Френкелю. Полная глубина потенциальной ямы обозначена на рисунке ΔE₀.

Мы рассмотрели упрощенный случай, когда все атомы имеют одинаковые значения величины ΔE и ΔE₀. В реальных кристаллах и особенно в поликристаллических телах можно наблюдать различную глубину потенциальных ям. Дефекты по Френкелю, в первую очередь, образуются за счет диссоциации ионов с малой глубиной потенциальной ямы.

Рассчитаем равновесную концентрацию дефектов по Френкелю. Для этого обозначим через N концентрацию ионов (узлов), способных к диссоциации - общее число узлов, то есть будем считать, что часть ионов в узлах уже продиссоциировала, а часть ионов находится в узлах и способна переходить в междоузлия.

Предположим, что в данный момент уже n ионов в единице объема находятся в междоузлиях. Следовательно, через n мы обозначим концентрацию дефектов по Френкелю, равную концентрации междоузельных «свободных» ионов.

Тогда концентрация ионов, находящихся в узлах, может быть вычислена как (N-n) – т.е. от общего числа ионов, способных к диссоциации в единице объема, мы вычитаем концентрацию междоузельных ионов. Эта разница равна концентрации ионов в узлах.

Вероятность диссоциации ω_д, т.е. перехода иона из узла в междоузлие при наличии n междоузельных ионов, будет пропорциональна числу ионов, находящихся в узлах, и вероятность того, что ион приобретает необходимую для такого перехода энергию за счет теплового движения, т.е. по статистике Больцмана-Максвелла пропорциональна .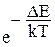

Таким образом вероятность «диссоциации» иона ω_д. Т.есть перехода его из узла в междоузлие равно:

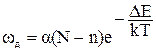(1),

где α – коэффициент пропорциональности.

Вероятность ω_p обратного процесса – процесса «рекомбинации» возвращения иона в пустой узел, будет пропорциональна числу ионов в междоузлиях n и числу пустых узлов, точнее, отношению числа пустых узлов к общему числу узлов:

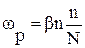(2) ,

где β – коэффициент пропорциональности.

В условиях равновесия имеем ω_д=ω_p:

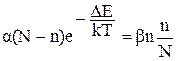
Учитывая, что концентрация ионов в междоузлиях оказывается существенно меньше концентрации узлов, можно предположить, что

(N-n) 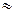N, тогда 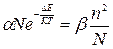; 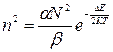и

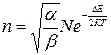(3)

Раскроем физический смысл α и β. Выразим концентрацию междоузельных ионов n через известные величины.

Для этого обозначим через N₁ – концентрацию возможных мест в междоузлиях. ω₁ – число способов, с помощью которых n ионов смогут разместиться по междоузлиям N₁, ω – число способов, с помощью которых n вакантных узлов смогут расположиться в узлах N.

Число этих способов будет равно:

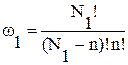(4)

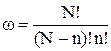(5)

При переходе ионов из узлов в междоузлия упорядоченность структуры уменьшается и энтропия системы растет. Изменение энтропии по сравнению с упорядоченным состоянием, при котором все ионы находятся в узлах, определяется согласно термодинамике формулой Больцмана:

ΔS=кln(ω ω₁) (6)

Где ωω₁ играет роль термодинамической вероятности, при которой «события» отражаются через ω и ω₁ ?.

Увеличение внутренней энергии единицы объема кристалла при переходе n ионов в междоузлия равно:

ΔU= ΔEn (7),

где ΔE – энергия диссоциации одного иона.

Свободная энергия кристалла определяется выражением:

F=U-TS (8)

Условию динамического равновесия процессов диссоциации и рекомбинации при заданной температуре соответствует минимум свободной энергии, значит, для равновесия имеем.

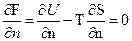(9)

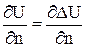Но и 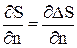, следовательно:

, ()

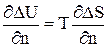С другой стороны из (7) следует:

, ()

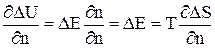тогда подставляя () в () получим:

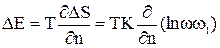(10)

Для вычисления факториалов в (4) и (5) воспользуемся формулой Стирлинга, которая для x>>1 имеет вид: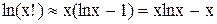

Подставим () и () в () и сделаем ряд математических преобразований:

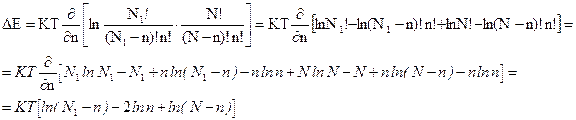
Полученное выражение позволяет найти равновесную концентрацию точечных дефектов:

, ()

, ()

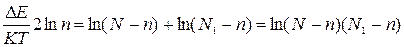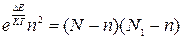при условии, чтоN>>n и N₁>>n получим

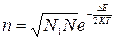(11)

Таким образом, мы получили формулу, выражающую концентрацию междоузельных ионов или концентрацию дефектов по Френкелю.

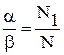, следовательно 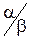равно отношению концентрации междоузлий и узлов.

Заметим, что формула (11)получена для монокристаллов. При этом полагают, что рекомбинация междоузельного иона может произойти лишь с вакансией в узле.

В поликристаллических телах рекомбинация, т.е. захват ионов в глубокую потенциальную яму может произойти на различных дефектах. Концентрация дефектов оказывается настолько велика, что рекомбинация не зависит от этой концентрации, а определяется лишь концентрацией междоузельных ионов n. Тепловая активация таких ионов пропорциональна общему числу ионов и вероятности тепловой энергии. При этом концентрация дефектов определяется соотношением:

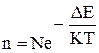(12)

Дефекты по Шоттки

Дефекты по Шоттки - есть пустые узлы, образовавшиеся за счет диссоциации ионов и перехода их на поверхность тела эстафетным путем. В атомных кристаллах дефекты по Шоттки могут быть одинарными, в полярных (ионных) - двойными.

Рисунок 2

Поскольку при дефектообразовании не нарушается электронейтральность, то более вероятно образование парных дефектов по Шоттки, т.е. положительных и отрицательных вакансий в ионных кристаллах. Тем не менее, обычно рассматривают и концентрацию возможных одинарных дефектов по Шоттки, не касаясь вопроса о способе, с помощью которого в том или ином случае в атомных кристаллических телах сохраняется электронейтральность.

Для создания одинарного дефекта по Шоттки требуется затратить энергию Δ E_ш, которая оказывается равной примерно половине полной энергии, необходимой для отрыва атома от кристалла.

Для создания парного дефекта по Шоттки требуется затратить энергию, которую будем обозначать через Δ E_p.

Не исключена возможность образования антишоттовских дефектов – лишних ионов в междоузлиях, внедрившихся с поверхности кристалла. Однако концентрация таких дефектов относительно мала.

Для расчета равновесной концентрации одинарных дефектов Шоттки обозначим через n₁ – концентрацию дефектов Шоттки; ω_ш- число способов, с помощью которых n₁ одинарных дефектов (вакансий) смогут разместиться в N узлах.

Число этих способов будет равно:

, ()

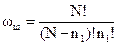Изменение энтропии по сравнению с упорядоченным состоянием, при котором все ионы находятся в узлах с учетом () определяется выражением:

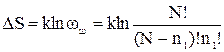, (6)

Увеличение внутренней энергии единицы объема кристалла при переходе n ионов в междоузлия равно:

ΔU= ΔE_шn (7),

Условию динамического равновесия процессов диссоциации и рекомбинации при заданной температуре соответствует минимум свободной энергии, значит, для равновесия имеем.

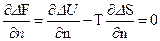, (9)

Подставим полученные выражения () и () в ():

, ()

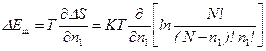Продифференцируем полученное выражение и раскроем факториалы. При условии, что равновесная концентрация дефектов Шоттки намного меньше концентрации узлов решетки N>>n₁ получим, что равновесная концентрация дефектов по Шоттки равна:

, ()

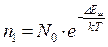Расчет равновесной концентрации парных дефектов по Шоттки аналогичен. Для этого обозначим как и ранее через N концентрацию узлов определенного знака (например положительных), способных к диссоциации. Через N` - концентрацию узлов другого знака, так же способных к диссоциации (и переходу на поверхность).

Концентрация парных дефектов по Шоттки n_р будет определяться ω_р- число способов, с помощью которых n_р парных дефектов (вакансий) смогут разместиться в N узлах и аналогично число способов ω′_р, с помощью которых n_р парных дефектов (вакансий) смогут разместиться в N` узлах:

, ()

, ()

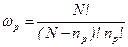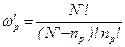Пользуясь методами расчета, используемыми ранее, можно подсчитать концентрацию парных дефектов:

, ()

, ()

, ()

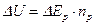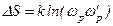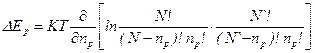Раскроем факториалы и проведем дифференцирование выражения () и получим формулу для расчета равновесной концентрации парных дефектов по Шоттки:

, ()

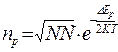Легко видеть, что концентрация парных дефектов по Шоттки вычисляется подобно концентрации дефектов по Френкелю, отличие в величинах энергий образования дефектов ΔE и ΔE_p , а также в величинах N₁ – (концентрация междоузлий) и N` - (концентрация узлов, где размешаются ионы, противоположные по знаку, по сравнению с ионами в узлах N).

Отношение концентраций дефектов по Френкелю и Шоттки определяются в основномвеличинами их энергии образования дефектов ΔE, ΔE_ш или ΔE_p. В большинстве случаев в реальных системах наблюдались преимущественно либо дефекты по Френкелю, либо парные дефекты по Шоттки.