Изотермический процесс
Изотермический процесс- процесс, при котором температура рабочего тела остается постоянной:
1) Уравнение процесса в дифференциальной форме:
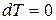 ,
, 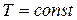 .
.
2) График процесса в системе координат 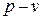 – равнобокая гипербола. Кривая процесса называется изотермой. (см. рисунок 3.1.)
– равнобокая гипербола. Кривая процесса называется изотермой. (см. рисунок 3.1.)
3) Соотношение между параметрами в процессе.
Из уравнения состояния идеального газа
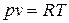 при
при 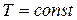
получаем
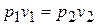 и
и 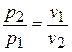 .
.
Это соотношение называется законом Бойля-Мариотта.
При постоянной температуре объем газа изменяется обратно пропорционально его давлению.
4) Теплоемкость рабочего тела в процессе
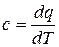 т.к.
т.к. 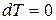
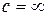
5) Изменение внутренней энергии и энтальпии в процессе
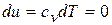 ;
;
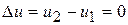 ,
, 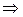
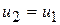 ;
;
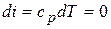 ;
;
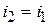 .
.
6) Работа расширения 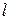 и располагаемая работа
и располагаемая работа 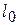 (полезная внешняя работа, которая может быть передана внешнему объекту работы) процесса:
(полезная внешняя работа, которая может быть передана внешнему объекту работы) процесса:
а) 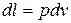 ,
,
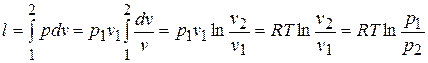 ,
,
т.к. из уравнения изотермы 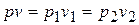 или
или 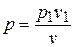
б) 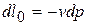 ,
, 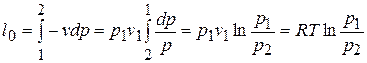 ,
,
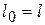
т.е. в изотермическом процессе идеального газа располагаемая работа численно равна работе объемного расширения.
7) Количество тепла, участвующего в процессе.
Основное уравнение первого закона термодинамики при 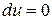 принимает вид
принимает вид
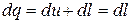 ,
,
количество теплоты участвующее в процессе
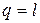 ,
,
8) Особенности превращения энергии в процессе
Вся энергия, подведенная в виде теплоты, расходуется на совершение работы.
9) Изменение энтропии в процессе
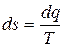 ,
, 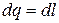
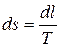 ;
;
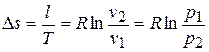 .
.
10) График процесса в системе координат  (тепловая диаграмма)– прямая параллельная оси удельной энтропии. (см. рисунок 3.2.)
(тепловая диаграмма)– прямая параллельная оси удельной энтропии. (см. рисунок 3.2.)
Теплота не тратится на изменение внутренней энергии.
Адиабатный процесс
Адиабатный - процесс протекающий в теплоизолированной системе. Для получения адиабатного процесса необходимым и обязательным условием является 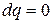 и, следовательно,
и, следовательно, 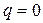 .
.
Обратимый адиабатный процесс можно осуществить в цилиндре с абсолютно нетеплопроводными стенками при бесконечно медленном перемещении поршня.
1) Уравнение процесса в дифференциальной форме:
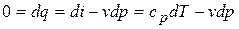 ,
, 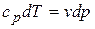 ;
;
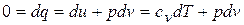 ,
, 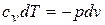 ;
;
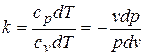
– показатель адиабаты;
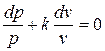 .
.
В интегральной форме уравнение процесса имеет вид:
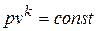 ,
,
2) График процесса в системе координат 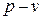 – не равнобокая гипербола, идущая более круто, чем изотерма, т.к. показатель адиабаты всегда больше единицы. Кривая процесса называется адиабатой. (см. рисунок 3.1.)
– не равнобокая гипербола, идущая более круто, чем изотерма, т.к. показатель адиабаты всегда больше единицы. Кривая процесса называется адиабатой. (см. рисунок 3.1.)
3) Соотношение между параметрами в процессе.
Из уравнения адиабаты следует, что
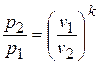 или
или 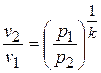 .
.
Если эти соотношения параметров тела подставить в уравнение состояния для крайних точек процесса 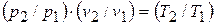 , то найдем
, то найдем
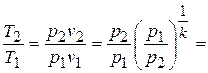
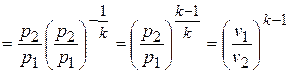
или
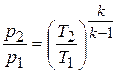
4) Теплоемкость рабочего тела в процессе
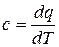 т.к.
т.к. 
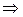
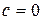
5) Изменение внутренней энергии и энтальпии в процессе
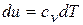 ,
,
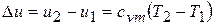 ,
,
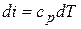 ,
,
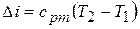 .
.
6) Работа расширения 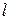 и располагаемая работа
и располагаемая работа 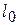 :
:
а) т.к.
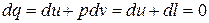 ,
,
то
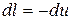
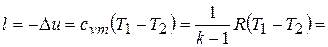
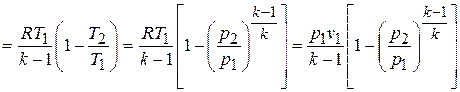 ,
,
б) т.к.
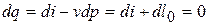 ,
,
то
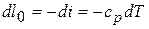 ;
;
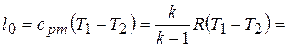
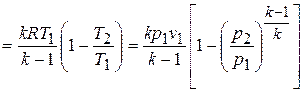 ,
,
таким образом
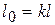
7) Количество тепла, участвующего в процессе.
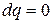 ,
,
количество теплоты участвующее в процессе
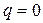 ,
,
8) Особенности превращения энергии в процессе
В адиабатном процессе работа расширения осуществляется за счет уменьшения внутренней энергии.
9) Изменение энтропии в процессе
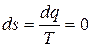 ,
,
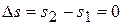 ,
,
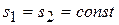 .
.
Энтропия в адиабатном процессе остается постоянной.
10) График процесса в системе координат  (тепловая диаграмма)– прямая параллельная оси абсолютных температур. (см. рисунок 3.2.)
(тепловая диаграмма)– прямая параллельная оси абсолютных температур. (см. рисунок 3.2.)
Равновесный адиабатный процесс является изоэнтропным.
Понятие адиабатный более широкое, чем изоэнтропный. Реальный, а следовательно неравновесный адиабатный процесс изоэнтропным не является.
Таблица 3.1
| Характеристика процесса | Процесс | ||||
| Изохорный | Изобарный | Изотермический | Адиабатный | Политропный | |
| Показатель политропы n | ∞ | k=cp/cv | n=(c-cp)/(c-cv) | ||
| Уравнение процесса | v=const p/T=const | p=const v/T=const | T=const Pv=const | pvk=const | pvn=const |
| Теплоемкость кДж/кгК | cv | cp | ∞ | cn=cv(n-k)/(n-1) | |
| Изменение внутренней энергии Δu1-2=u2-u1 кДж/кг | cv(T2-T1) | cv(T2-T1) | cv(T2-T1) | cv(T2-T1) | |
| Изменение энтальпии Δi1-2=i2-i1 кДж/кг | cp(T2-T1) | cp(T2-T1) | cp(T2-T1) | cp(T2-T1) | |
| Изменение энтропии Δs1-2=s2-s1 кДж/кг | cvln T2/T1 | cpln T2/T1 | R ln v2/v1= = R ln p1/p2 | cv ln(T2/T1) + + R ln(v2/v1) | |
| Количество теплоты q1-2, кДж/кг | cv(T2-T1) | cp(T2-T1) | TΔs= RT ln v2/v1= = R ln p1/p2 | cn(T2-T1)= =cn(T2-T1) (n-k)/(n-1) | |
| Работа изменения объема l1-2, кДж/кг | p(v2-v1)= = R(T2-T1) | l1-2= l01-2= q1-2= = RT ln v2/v1= = R ln p1/p2 | l1-2=Δu1-2=
=(p1v1-p2v2)/(k-1)=
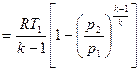
| (p1v1-p2v2)/(n-1)=
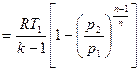
| |
| Располагаемая работа l01-2, кДж/кг | v(p1-p2)= = R(T1-T2) | l01-2= l1-2= q1-2= = RT ln v2/v1= = R ln p1/p2 | l01-2=-Δi1-2=k l1-2=
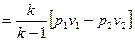
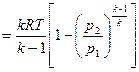
| l01-2=n l1-2=
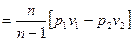
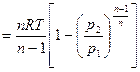
|
Дата добавления: 2020-03-21; просмотров: 1081;











