Термодинамические процессы идеального газа

Идеальный газ – это газ, строго подчиняющийся закону идеального газа

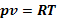(3.1.)

и его частицы представляют собой материальный точки, между которыми отсутствует силовое взаимодействие.

Термодинамическим процессом называют процесс изменения состояния системы в результате ее взаимодействия с ОС.

Политропный процесс – процесс, при котором доля тепла, идущая на изменение внутренней энергии рабочего тела, остается постоянной величиной. Ряд термодинамических процессов идеального газа (изобарный, изохорный, изотермический и адиабатный) можно считать частными случаями политропного процесса.

Равновесным процессом называют процесс, в ходе которого система проходит через бесконечное множество бесконечно близких равновесных состояний.

Количество теплоты, участвующее в политропном процессе, может быть выражено произведением теплоемкости процесса с на разность температур в начале и конце процесса:

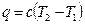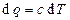и (3.2)

Уравнение политропного процесса выводится на основании совместного решения первой и второй форм записи первого закона термодинамики:

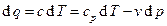, (3.3)

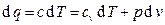(3.4)

из которых после несложных преобразований получаем:

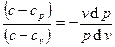(3.5)

Обозначив показатель политропы как n

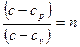(3.6)

получаем уравнение политропного процесса в дифференциальной форме:

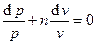(3.7)

откуда уравнение политропного процесса в интегральной форме имеет вид:

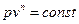(3.8)

Это уравнение используется для построения рабочей диаграммы (графического изображения процесса в p-v координатах) – см. рисунок 3.1.

Нетрудно заметить, что вид процесса определяется показателем процесса n.

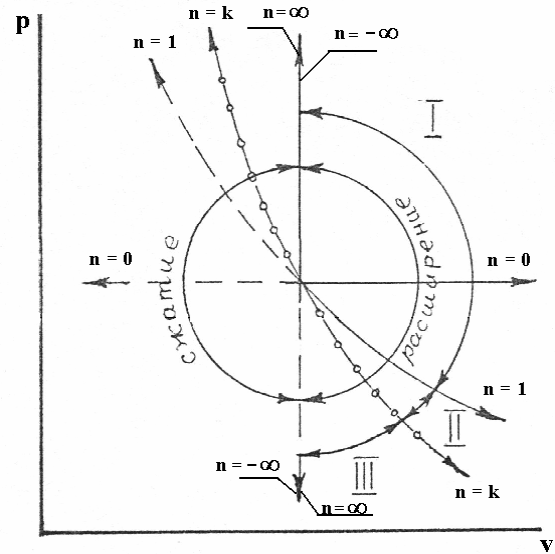
Рисунок 3.1 – различные частные случаи политропного процесса в p-v координатах: n=0 – изохорный; n=±∞ - изобарный; n=1 – изотермический n= k – адиабатный.

Решая совместно уравнение (3.8) и уравнение состояния (3.1), можно получить соотношения параметров в начале и конце процесса (см. табл. 3.1).

Изменение внутренней энергии газа определяется по формуле:

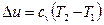(3.9)

Работа расширения l может быть найдена из первой формы записи уравнения первого закона термодинамики (2):

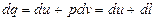, (3.10)

По определениям данных функций, dq=cdT и du=c_vdT, откуда

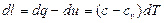(3.11)

После интегрирования и преобразований получаем:

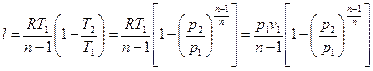,(3.12)

Располагаемая работа l₀ может быть найдена из второй формы записи первого закона термодинамики (3):

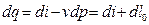(3.13)

По определениям данных функций, dq=cdT и di=c_pdT, откуда

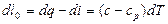(3.14)

После интегрирования и преобразований получаем:

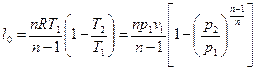, (3.15)

таким образом

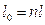
Изменение энтропии газа в политропном процессе определяется по формуле

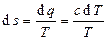(3.16)

или для конечного изменения состояния (т.к. k=с_p/с_v)

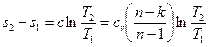(3.17)

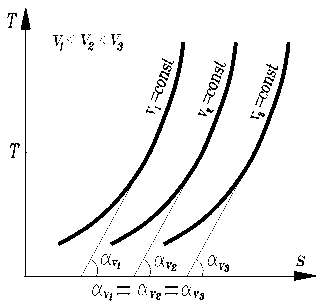
С помощью этого уравнения можно построить график процесса на тепловой диаграмме (в T-s координатах) – см. рисунок 3.2.

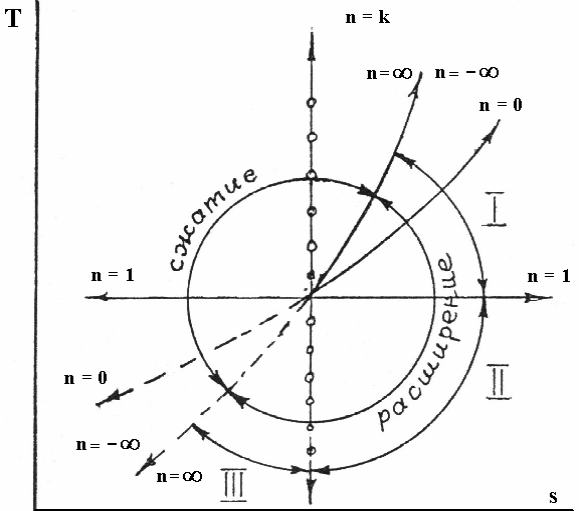
Рисунок 3.2 – различные частные случаи политропного процесса в T-s координатах: n=0 – изохорный; n=±∞ - изобарный; n=1 – изотермический n= k – адиабатный.

Особенности превращения энергии зависят от показателя политропы. Все процессы могут быть разделены на 3 характерные группы. Рассмотрим группы процессов в области расширения ( , )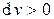

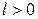1 группа,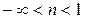

В процессах этой группы , , ,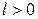

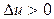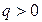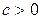
Таким образом в процессах этой группы при расширении теплота подводится и частично расходуется на совершение работы и увеличение энергии рабочего тела. С увеличением 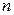возрастает доля тепла, идущая на совершение работы

2 группа,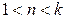

Для этих процессов , , ,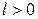

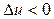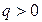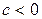
В процессах этой группы при расширении газа работа совершается как за счет подвода тепла так и за счет уменьшения внутренней энергии рабочего тела. С увеличением показателя политропы (от 1 до k) возрастает доля работы, совершаемая за счет внутренней энергии и уменьшается доля работы, совершаемая за счет подвода теплоты.

3 группа,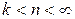

Для процессов этой группы , , ,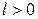

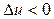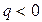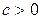
При расширении рабочего тела уменьшается его внутренняя энергия, часть ее расходуется на совершение работы, а часть отводится в виде теплоты; с увеличением показателя политропы увеличивается отвод теплоты за счет уменьшения количества совершенной работы.

При анализе тепловых машин часто вместо политропного процесса рассматривают его частные случаи – изобарный, изохорный, изотермический или адиабатный.

Изохорный процесс

Изохорный процесс– процесс, при котором объем ТДС не изменяется.

1) Уравнение процесса при независимых переменных , :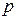

, .

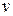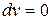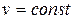2) График процесса в системе координат 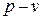– прямая параллельная оси давлений. Кривая процесса называется изохорой (см. рисунок 3.1.)

3) Соотношение между параметрами в процессе.

Из уравнения состояния идеального газа

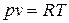при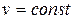

получаем

.

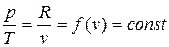При постоянном объеме давление газа изменяется прямо пропорционально абсолютным температурам:

.

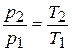4) Теплоемкость рабочего тела в процессе

.

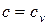5) Изменение внутренней энергии и энтальпии в процессе

;

;

;

.

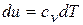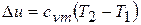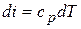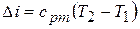6) Работа расширения 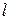и располагаемая работа 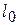(полезная внешняя работа, которая может быть передана внешнему объекту работы) процесса:

, ;

, ,

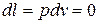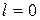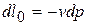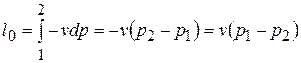на графике 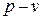располагаемая работа численно равна площади между линией процесса и осью давлений. Из полученного выражения видно, что полезная внешняя работа в изохорном процессе равна работе проталкивания 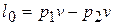. Например, проталкивание несжимаемой жидкости по каналу от одного сечения к другому.

7) Количество тепла, участвующего в процессе.

Основное уравнение первого закона термодинамики при 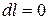принимает вид

,

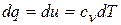количество теплоты участвующее в процессе

.

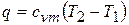8) Особенности превращения энергии в процессе

Вся энергия, подведенная к ТДС в форме теплоты, идет на увеличение внутренней энергии и температуры, работа расширения процесса равна нулю.

9) Изменение энтропии в процессе

,

.

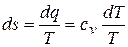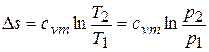10) График процесса в системе координат 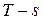(тепловая диаграмма)– логарифмическая кривая (см. рисунок 3.2.)

Подкасательная к кривой в любой ее точке дает значение истинной теплоемкости .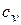

Изохоры, построенные для различных объемов, смещены одна относительно другой, и чем больше объем газа, тем дальше находится изохора от оси ординат.

Изобарный процесс

Изобарный процесс- процесс в котором давление в ТДС остается постоянным:

1) Уравнение процесса в дифференциальной форме:

, .

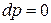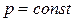2) График процесса в системе координат 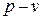– прямая параллельная оси объемов. Кривая процесса называется изобарой. (см. рисунок 3.1.)

3) Соотношение между параметрами в процессе.

Из уравнения состояния идеального газа

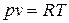при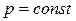

получаем

.

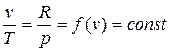Это соотношение называется законом Гей-Люссака.

При постоянном давлении объем газа изменяется прямо пропорционально абсолютным температурам:

.

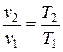4) Теплоемкость рабочего тела в процессе

.

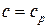5) Изменение внутренней энергии и энтальпии в процессе

;

;

;

.

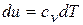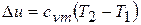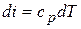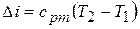6) Работа расширения 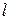и располагаемая работа 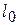(полезная внешняя работа, которая может быть передана внешнему объекту работы) процесса:

а) , ;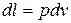

,

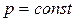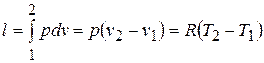на графике 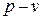работа объемного расширения численно равна площади между линией процесса и осью удельных объемов.

б) , ,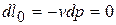

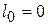т.е. располагаемая работа в изобарном процессе не совершается.

7) Количество тепла, участвующего в процессе.

Основное уравнение первого закона термодинамики при 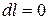принимает вид

,

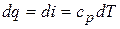количество теплоты участвующее в процессе

.

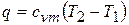8) Особенности превращения энергии в процессе

Теплота, подведенная к рабочему телу расходуется на изменение его энтальпии.

9) Изменение энтропии в процессе

,

.

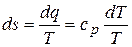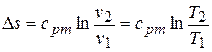10) График процесса в системе координат 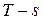(тепловая диаграмма)– логарифмическая кривая. (см. рисунок 3.2.)

Подкасательная к кривой в любой ее точке дает значение истинной теплоемкости .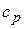

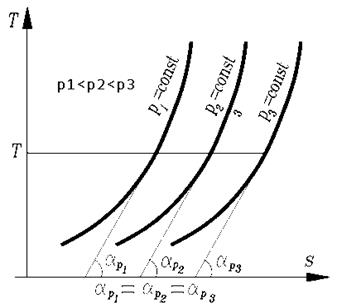
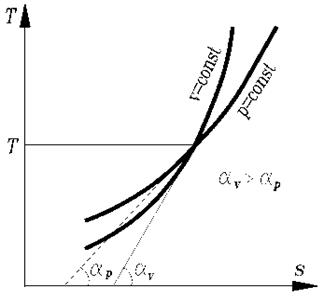
Изобары, построенные для различных давлений, смещены одна относительно другой и чем больше давление газа, тем ближе находится изобара к оси ординат.

Из сопоставления уравнений изменения энтропии в процессе следует, что в случае осуществления изохорного и изобарного процессов в одном интервале температур возрастание энтропии будет больше в изобарном процессе, т.к. 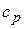всегда больше .

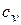Изобары являются более пологими кривыми, чем изохоры.