Основные уравнения и допущения
Допущения:
1 Будем рассматривать установившееся или стационарное движение рабочего тела, при котором параметры в каждой точке т.д.с. не изменяются со временем.
2 Будем рассматривать движение рабочего тела, при котором параметры в поперечном сечении постоянны. Они изменяются только вдоль потока (вдоль одной оси)
При этих допущениях основные уравнения будут иметь вид:
Уравнение неразрывности потока (по сути является закон сохранения массы):
Расход рабочего тела через каждое поперечное сечение канала постоянен.
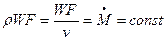
где 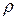 – плотность потока;
– плотность потока; 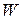 – скорость потока;
– скорость потока; 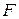 – площадь поперечного сечения канала;
– площадь поперечного сечения канала; 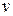 – удельный объем;
– удельный объем; 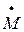 – массовый расход газа.
– массовый расход газа.
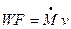
– уравнение неразрывности в интегральной форме
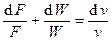
– уравнение неразрывности в дифференциальной форме
Уравнение I закона термодинамики для потока (выражает собой закон сохранения энергии). Энергия открытой системы Е изменяется за счет взаимодействия с ОС в виде теплоты Q, технической работы 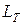 , массообмена М. Поступая в систему через контрольную поверхность F1 масса обладает запасом удельной внутренней энергии u, удельной кинетической энергией
, массообмена М. Поступая в систему через контрольную поверхность F1 масса обладает запасом удельной внутренней энергии u, удельной кинетической энергией 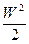 и удельной потенциальной энергией
и удельной потенциальной энергией 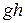 , так что полный запас удельной энергии
, так что полный запас удельной энергии
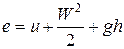
кроме того, при вводе рабочего тела в систему совершается работа (работа проталкивания), равная произведению силы 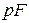 на перемещение
на перемещение 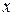
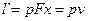
Тогда изменение полной энергии системы имеет вид
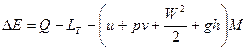
– закон сохранения энергии
учитывая, что 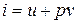 при стационарном режиме течения
при стационарном режиме течения 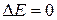 для проточной ТДС для удельных величин
для проточной ТДС для удельных величин
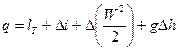
– уравнение I закона т.д. для потока в интегральной форме
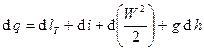
– уравнение I закона т.д. для потока в дифференциальной форме
Кинетическая и потенциальная энергии потока вещества, которыми обменивается ТДС с ОС, могут быть полностью превращены в работу, поэтому удельная располагаемая работа открытой системы представляет собой сумму этих видов энергии и работ
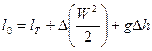
тогда уравнение приводится к виду
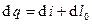
Т.к. обычно размеры устройств (сопла и диффузора) малы, а плотности газов невелики, то изменением потенциальной энергии можно пренебречь. Если кроме того поток не совершает технической работы 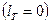 , то
, то
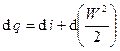
– уравнение I закона т.д. для потока
Располагаемая работа 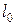 в этом случае полностью определяется изменением кинетической энергии потока, поэтому
в этом случае полностью определяется изменением кинетической энергии потока, поэтому
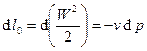
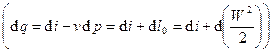
или раскрывая дифференциал получим
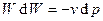
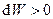 ,
, 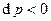 ;
;
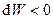 ,
, 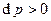
Если время пребывания газа в канале мало, то течение в нем может быть, в первом приближении, принято адиабатным 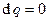 . Тогда можно записать
. Тогда можно записать
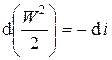
– уравнение I закона т.д. для адиабатного потока в дифференциальной форме
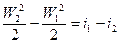
– уравнение I закона т.д. для адиабатного потока в интегральной форме
Это уравнение показывает, что увеличение скорости потока происходит за счет уменьшения энтальпии и наоборот
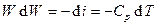
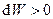 ,
, 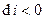 ,
, 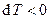 ;
;
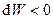 ,
, 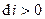 ,
, 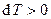 .
.
Дата добавления: 2020-03-21; просмотров: 895;











