Частица в одномерной прямоугольной «потенциальной яме»

Такая «яма» описывается потенциальной энергией вида

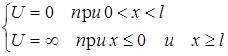
При таком условии частица не проникает за

пределы "ямы", т.е. y(0)= y(l)=0. (27)

В пределах ямы (0<x<l) уравнение (22) сведется к уравнению

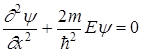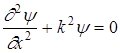или , (28)

где k²= 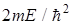. Общее решение (28) y(х)=Аsinkx+Bcoskx.(29)

Так как согласно (27) ψ(0)=0, то В=0, тогда y(х)=Аsinkx . (30)

Условие (27) y(l)=Аsinkl=0 выполняется только при kl=pn, где n=1,2...целые числа, т.е. необходимо, чтобы k=pn/l. (31)

Из (29) и (31) следует, что 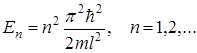(32)

Таким образом, энергия в «потенциальной яме» принимает лишь определенные, дискретные значения, т.е. квантуется. Квантованные значения энергии Е_n называются уровнями энергии, а число n, определяющее энергетические уровни, называется главным квантовым числом.

Заметим, что n=1 cоответствует минимальная энергия Е₁¹0.

Подставив в (30) значения k из (31), найдем собственные функции

.

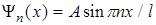Постоянную А найдем из условия нормировки (18), которое для данного случая имеет вид

.

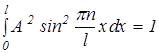В результате интегрирования получим 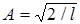, а собственные функции будут иметь вид

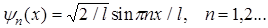(33)

Графики этих функций, соответствующие уровням энергии при n=1, 2, 3, приведены на рис. 5 (а). На рис. 5 (б) изображены плотности вероятности обнаружения частицы на различных расстояниях от «стенок» ямы

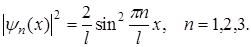
Из рис. следует, что, например, в квантовом состоянии с n=2 частица не может находится в середине «ямы», в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траектории частицы в квантовой механике несостоятельны.