Квантовый осциллятор

Классическим осциллятором в классической механике называли частицу массой m, колеблющуюся с частотой w₀=Ök/m под действием упругой силы F=-kx.

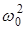Потенциальная энергия такой частицы U=kx²/2=m x²/2; в точках с координатами ±х_max она равна полной энергии Е. Т.о., энергия частицы могла принимать любые значения, т.е. изменяться непрерывно (рис.6).

В квантовой механике понятие силы не используется, поэтому квантовый осциллятор следует определить как частицу с потенциальной энергией U=kx²/2=m 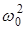x²/2. (34)

Подставляя (34) в (22) и учитывая, что частица движется только вдоль одной прямой (вдоль оси х), получим

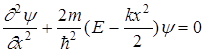. (35)

Решая уравнение (35), можно получить, что энергия (энергетический уровень) частицы принимает только дискретные значения (квантуется).

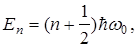(36)

n=0, 1, 2... – квантовые числа.

Наименьшее значение энергии E₀= 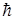w₀/2 определяется только собственной частотой w₀ и ее невозможно отнять у частицы никаким охлаждением, она сохранилась бы и при Т=0К.

Из (36) следует, что уровни находятся на равных расстояниях друг от друга

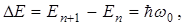(37)

т.е. уровни эквидистантны [см. рис. 7, где на границе с потенциальной кривой U(±х_max)=Е_n]. При больших квантовых числах n DЕ/Е_n=1/(n+1/2)®0, т.е. происходит относительное сближение энергетических уровней и получаются результаты, близкие к результатам классического рассмотрения, когда энергия частицы может изменяться непрерывно, и, следовательно, может иметь любые значения. В этом заключается принцип соответствия, сформулированный Бором в 1923 г.:

При больших квантовых числах выводы и результаты квантовой механики должны соответствовать выводам и результатам классической механики.

Более общая трактовка принципа соответствия заключается в следующем: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применения. Причем в определенных, предельных случаях, новая теория переходит в старую.