Собственные функции и собственные значения. Свободная частица

Функции Y,удовлетворяющие уравнению Шредингера при данных U, называются собственными функциями.

Значения Е, при которых существуют решения уравнения (22), называются собственными значениями.

В качестве примера определим y и Е для свободной частицы.

Свободной называют частицу, на которую не действуют силы, т.е. 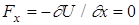. Следовательно, U(x)=const и ее можно принять равной нулю. Таким образом, в случае свободного движения частицы, ее полная энергия совпадает с кинетической, а скорость 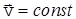. Направим ось Х вдоль вектора 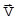. Тогда (22) можно записать в виде

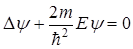. (23)

Прямой подстановкой можно убедится, что частным решением этого уравнения является функция y(х)=Аexp(ikx), где А=сonst, k=const c собственным значением энергии

Е= 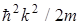. (24)

C учетом (21) волновая функция

Y(х)=Аexp(-iwt+ ikx)= Аexp[-(i/ 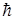)(Еt- р_xх)]. (25)

здесь w=Е/ 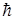, k=р_x/ .

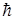Функция (25) представляет собой плоскую монохроматическую волну де Бройля [cм. (16)].

Из (24) следует, что зависимость энергии от импульса

Е= 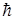²k²/(2m)=Р_х²/(2m)=mv²/2 (26)

оказывается обычной для нерелятивиских частиц. Следовательно, энергия свободной частицы может принимать любые значения, т.е. ее энергетический спектр является непрерывным.

Плотность вероятности обнаружить частицу в данной точке пространства

çy÷ ²=yy^*=A²,

т.е. все положения свободной частицы в пространстве являются равновероятными.