В областях (I, III) это бегущие плоские волны, а в области (II)- затухающая волна.
Движение частиц через потенциальный барьер. Туннельный эффект.
Рассмотрим одномерное движение. В этом простейшем случае уже проявляются принципиальные отличия движения микрочастиц от классического. При одномерном движении рассеяние означает изменение направления движения на противоположное. Пусть на пути частиц расположен потенциальный барьер конечной ширины, в области барьера и вне его 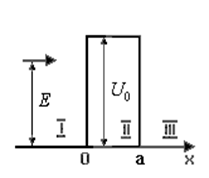
Рис. 1.3 Конфигурация потенциальной энергии.
потенциальные энергии частицы постоянны, но эти потенциальные энергии различаются на конечную величину. Мы предположим, что на границе потенциальная энергия меняется скачком (рис.1.3). В реально встречающихся условиях переход, конечно, плавный. Выберем систему координат так, чтобы ось x была параллельна направлению движения частицы. Изменение потенциальной энергии по оси x описывается формулой
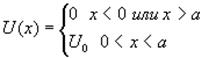 .
.
На рисунке горизонтальная стрелка показывает начальное направление движения частиц, а ее положение по вертикали - энергию частиц.
В случае, когда полная энергия частицы E больше ее потенциальной энергии U0 в области II, на границе происходит частичное рассеяние. Рассмотрим ситуацию, когда E < U0. Классическая частица, подходя к барьеру, высота которого больше ее полной энергии, отражается от него. Пройти через такой барьер, т.е. через область, в которой ее кинетическая энергия стала бы отрицательной, она не может.
Рассмотрим квантовомеханическое решение. Всю область изменения переменной x разобьем на три (см. рисунок). Поскольку при заданных условиях потенциальная энергия U не может быть записана в виде аналитической функции, мы напишем уравнение Шредингера отдельно для областей (I), (III) (где потенциальные энергии одинаковы, U0 = 0) и для области (II) и найдем решения в обоих случаях, т.е. функции Ψ1, 3 и Ψ2. На границе при x = 0 в силу непрерывности волновой функции и ее производной приравняем Ψ1 и Ψ2 и их первые производные:
для областей (I, III)
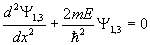 , (1.6) , (1.6)
|
для области (II)
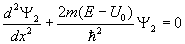 , (1.7) , (1.7)
|
где m и E – масса и полная энергия частицы, соответственно. Введем обозначения
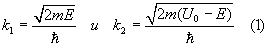 (1.8) (1.8)
|
Уравнения приобретают вид
|
Общие решения уравнений (1) таковы:
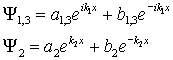 (1.10) (1.10)
|
В областях (I, III) это бегущие плоские волны, а в области (II)- затухающая волна.
в области (III) потенциал постоянен, отражения нет, и коэффициент b3 = 0.
Коэффициент прохождения D:
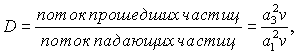
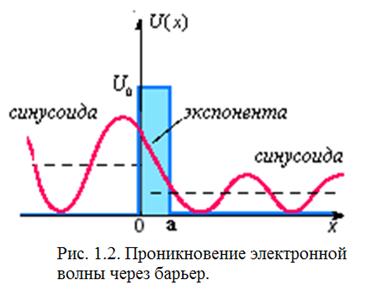
где v - скорость частицы. Она одинакова для всех частиц в областях I и III.
Волновая функция (рис.1.2) отлична от нуля во всех трех областях. Внутри барьера она экспоненциально затухает, поэтому вероятность прохождения значительно меньше единицы. Это прохождение сквозь запрещенную классической механикой область и называют "туннельным эффектом".
Коэффициент прохождения через барьер прямоугольной формы
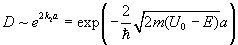 . (1.11) . (1.11)
|
Эта формула показывает, во-первых, что коэффициент прохождения не равен нулю, во-вторых, его величина очень сильно зависит от ширины барьера a.
Прошедшая волна зависит также от соотношения высоты барьера и энергии частиц, от ширины барьера и его формы.
| <== предыдущая лекция | | | следующая лекция ==> |
| Контакт металл-полупроводник: выпрямляющий (барьер Шотки) и невыпрямляющий (омический) контакты | | |
Дата добавления: 2017-01-26; просмотров: 1478;

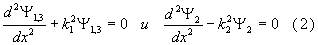 (1.9)
(1.9)










