Записать окончательное выражение решения и построить его график
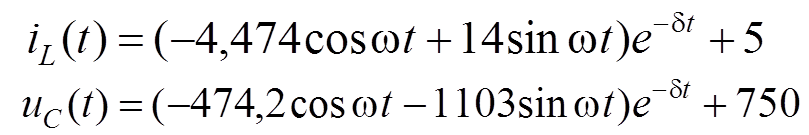
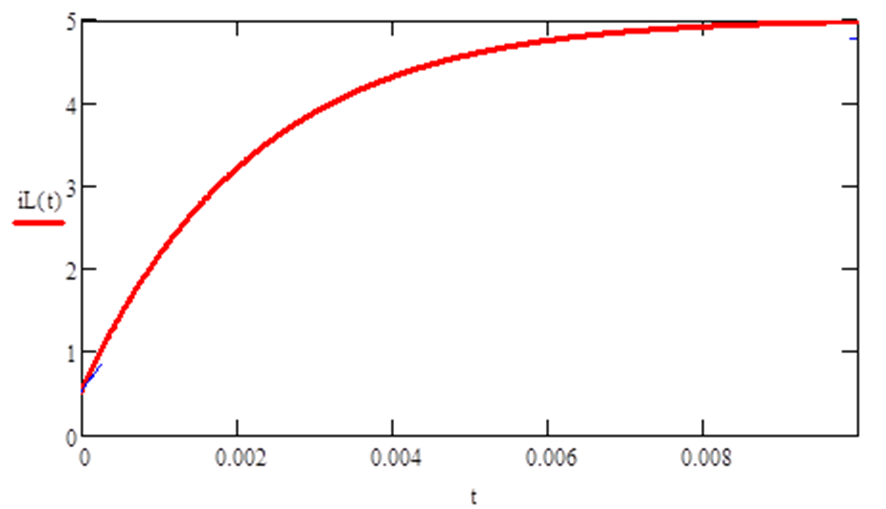
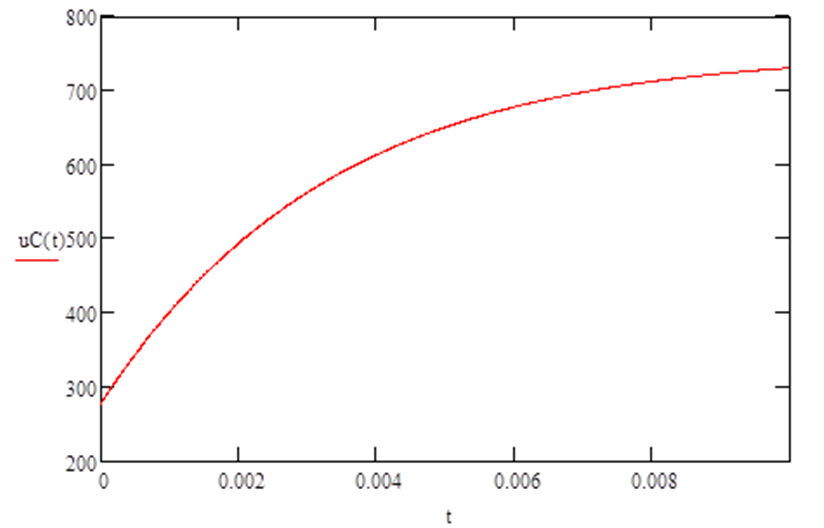
Из рассмотренного примера расчета переходного процесса для цепи с двумя реактивными элементами можно сделать вывод, что если все корни характеристического уравнения – действительные числа, переходный процесс носит апериодический характер. Если корни комплексные сопряженные , то переходный процесс имеет колебательный характер.
В системах автоматического регулирования колебания под действием управляющих сигналов, т.е. в течение переходных процессов, как правило не допускаются. Поэтому анализ корней характеристического уравнения системы управления имеет важное значение.
Апериодический или колебательный характер переходного процесса в цепи второго порядка (с двумя реактивными элементами) можно обьяснить физикой энергетических явлений в цепи во время переходного процесса. На момент коммутации реактивные элементы схемы (индуктивности и емкости) имели запас энергии. В емкости – это энергия электрического поля конденсатора, в индуктивности - это энергия магнитного поля катушки. В новом установившемся режиме величина этих энергий примет другие значения. В процессе перехода цепи к новому установившемуся состоянию емкость и индуктивность будут обмениваться энергиями между собой, создавая перетоки своих энергий. Кроме этого часть запаса энергии реактивных элементов будет преобразовываться в тепловую энергию, выделяющююся на резисторах схемы. При достаточно большом активном сопротивлении цепи вся запасенная реактивная энергия успеет превратиться в тепло, не оставляя шансов на взаимный переток энергий от каушки к емкости и (или) наоборот. Этот режим переходного процесса называеся апериодическим и свободная составляющая тока не успевает изменить направление протекания на противоположное, то есть стать отрицательным. Оценить возможность появления в цепи апериодического процесса можно по виду корней характеристического уравнения. Апериодический режим соответствует вещественным отрицательным корням.
Если активное сопротивление цепи сделать достаточно малым, тогда преобразование энергии реактивных элементов в тепло уменьшится, и появятся перетоки энегиц от конденсатора к катушке и наоборот. В конденсаторе, например, при отдаче своей энергии полярность заряженных обкладок будет противоположна полярности, соответствующей приему энергии. Это приведет к изменению направления тока в емкости. То есть переходной процесс будет носить характер колебаний, поэтому он называется колебательный.
Колебательный режим соответствует комплексным сопряженным корням характеристического уравнения.
В процессе колебательного переходного режима свободная составляющая переходного тока имеет вид синусоиды с уменьшающейся с течением времени амплитудой (затухающая синусоида). Количественно величина затухания этой синусоиды оценивается так называемым декрементом колебаний  . Декремент колебаний равен отношению двух амплитуд затухающей синусоиды, отстоящих друг от друга на время периода колебания - T.
. Декремент колебаний равен отношению двух амплитуд затухающей синусоиды, отстоящих друг от друга на время периода колебания - T.

Здесь 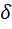 вещественная часть одного из комплексных корней характеристического уравнения
вещественная часть одного из комплексных корней характеристического уравнения
 где
где 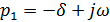 ,
,
а T связано с мнимой частью корня 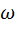
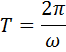
Понятие декремента колебаний может быть использовано для экспериментального определения корней характеристического уравнения цепи по осциллограме переходного тока или напряжения. Для этого из осциллограммы следует взять амплитуды двух следующих друг за другом колебаний и период колебаний. Тогда

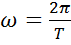

В этих расчетах используется логарифмический декремент колебаний 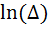 .
.
Дата добавления: 2020-03-21; просмотров: 986;











