Неравномерная нагрузка фаз.

Соединение звездой. При неравномерной нагрузке фаз, когда I_А ≠ I_В≠ I_С , в нулевом проводе трехфазной системы, соединенной звездой, течет уравнительный ток I₀.

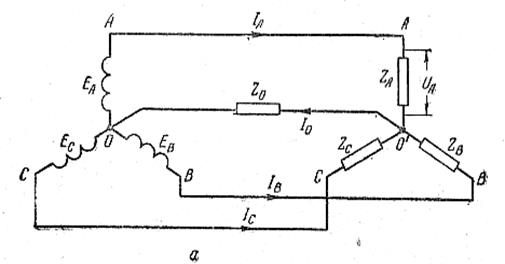
Но ток в участке цепи может течь лишь в том случае, когда на его концах есть разность потенциалов. Следовательно, при неравномерной нагрузке фаз между точками О и О′ возникает разность потенциалов (напряжение). Напряжение между нулевыми точками генераторов и нагрузки называют смещением нейтрали ( U₀ ). Из схемы

U₀ = I₀ z₀,

где z₀ – сопротивление нулевого провода.

Смещение нейтрали оказывает сильное влияние на работу нагрузки. По второму правилу Кирхгофа, для контура ОАА′О′О

Ė_А = Ů_А = Ů₀,

откуда

Ů_А = Ė_А - Ů₀.

Рассуждая совершенно аналогично для контуров ОВВ′О′О и ОСС′О′О, получим подобные выражения для Ů_В и Ů_С.

Ů_А = Ė_А - Ů₀;

Ů_В = Ė_В - Ů₀;

Ů_С = Ė_С - Ů_0.

Построим векторную диаграмму этих величин. Для этого отложим векторы фазных э. д. с., которые равны по величине и направлены под углом 120⁰ друг к другу, и вектор смещения нейтрали, который тоже имеет некоторые величину и направление.

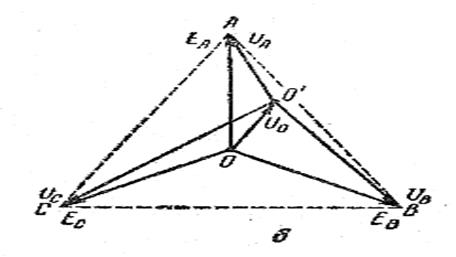
Из формулы Ė_А = Ů_А = Ů₀ следует, что Ē_А можно получить, если к Ū₀ пристроить Ū_А, а из диаграммы видно, что для получения Ē_А к Ū₀ надо пристроить отрезок О′А. Следовательно, этот отрезок и будет выражать Ū_А. Рассуждая аналогично в отношении э. д. с. Е_В и Е_С, придем к выводу, что отрезок О′В изображает Ū_В, а отрезок О′С изображает Ū_С.

Из этой диаграммы видно, что напряжения на фазах оказываются неодинаковыми, наступает так называемый перекос фазных напряжений. Перекос фазных напряжений – явление весьма нежелательное, оно нарушает работу отдельных фаз. Из этой же диаграммы следует, что причиной перекоса является смещения нейтрали, и чем больше Ū₀, тем разница между фазными напряжениями больше, чем меньше Ū₀, тем фазные напряжения более симметричны, и если Ū₀ = 0, то точка О′ сольется с О и фазные напряжения станут совершенно одинаковы. Следовательно, при эксплуатации трехфазных систем надо стремиться к тому, чтобы смещение нейтрали было возможно меньше.

Из формулы U₀ = I₀ z₀ следует, что для уменьшения U₀ надо уменьшать либо I₀, либо z₀. Уменьшить уравнительный ток I₀ можно, выравнивая нагрузку фаз. Если это по каким-либо причинам невозможно, а смещение нейтрали слишком велико, то надо уменьшать сопротивление нулевого провода z₀, то есть увеличивать его сечение, железный провод заменять алюминиевым или медным.

Если потенциал нулевой точки генератора принять равным нулю и посчитать , что на диаграмме ей соответствует точка О, то любая другая точка на этой диаграмме будет соответствовать совершенно определенной точке цепи и отрезок, соединяющий две любые точки на диаграмме, будет определять по величине и фазе напряжения между соответствующими точками цепи.

Такая диаграмма, любая точка которой соответствует определенной точке цепи, называется топографической. На рисунке

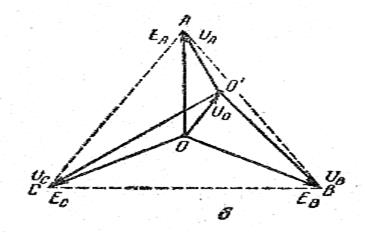
точка О′ соответствует нулевой точке нагрузки, точки А, В и С – точкам А, В, и С цепи, отрезок ОО′ отображает смещение нейтрали, отрезки АВ, ВС и СА – линейные напряжения U_АВ, U_ВС, U_СА и т.д.

Расчет трехфазной системы, соединенной звездой. Под расчетом трехфазной системы подразумевают определение фазных и линейных токов, фазных напряжений, потребляемой мощности, коэффициента мощности, а при необходимости и ряда других величин.

При этом заданными обычно являются фазные э. д. с. источника тока, его внутреннее сопротивление, сопротивления проводов и фаз нагрузки.

Трехфазная система, соединенная звездой, представляет собой цепь с двумя узловыми точками. Следовательно, трехфазную систему, соединенную звездой, можно рассчитывать методом узлового напряжения, только оперировать следует не абсолютными значениями величин, а их комплексными выражениями.

Попытка определить фазные токи ( а следовательно, и линейные ) по формуле

I_Ф = U_Ф

z

приведет к неверным результатам, так как при неравномерной нагрузке фаз фазные напряжения неодинаковы и нам не известны. Порядок расчета лучше всего проследить на примере.

Пример. Определить линейные токи и напряжения на фазах нагрузки, которая питается от трехфазного генератора, с фазными э. д. с. Е_Ф = 220 в и внутренним сопротивлением Х_Lо = 1 ом, если сопротивления фазных проводов чисто активные, R_пр = 2 ом, сопротивление нулевого провода Z_о = ( 1+ j2 ) Ом, а сопротивление фаз нагрузки выражается комплексами:

Z_А = ( 3 + j4 ) ом, Z_В = ( 6 + j5 ) ом, Z_С = ( 5 + j6 ) Ом

Решение. Выразим фазные э. д. с. в комплексной форме. Направим Ē_А по действительной оси, тогда

Ė_А = 220 в, Ė_В = 220_е^-j120о = 220 ( - 0,5 – j0,87 ) = ( - 110 – j192 ) в,

Ė_С = 220е^120о = 220 ( - 0,5 + j0,87 ) = ( - 110 + j192 ) в.

«Внесем» внутренние сопротивления фаз генератора и сопротивления фазных проводов в нагрузку. Сопротивление и проводимость фазы нагрузки с «внесенными» туда сопротивлениями обозначим знаком штрих.

Z′_А = Z_А + jХ_Lо + R_пр = 3 + j4 + j1 + 2 = ( 5 + j5 ) ом;

Z′_В = Z_В + jХ_Lо + R_пр = 6 + j5 + j1 + 2 = ( 8 + j6 ) ом;

Z′_С = Z_С + jХ_Lо + R_пр = 5 + j6 + j1 + 2 = ( 7 + j7 ) ом.

Определим проводимость ветвей:

Y′_А = _1_ = _1__ = ( 0,1 – j0,1 ) сим;

Z′_А 5 + j5

Y′_В = _1_ = _1__ = ( 0,08 – j0,06 ) сим;

Z′_В 8 + j6

Y′_С = _1_ = _1__ = ( 0,07 – j0,07 ) сим;

Z′_С 7 + j7

Y′₀ = _1_ = _1__ = ( 0,2 – j0,4 ) сим.

Z₀ 1+ j2

Определяем смещение нейтрали (узловое напряжение):

Ů₀ = Ė_АY′_А_+_ Ė_ВY′_В_+ Ė_СY′_С =

Y′_А + Y′_В + Y′_А + Y₀

= 220 ( 0,1 – j0,1 ) + ( - 110 – j192 ) ∙ (0,08 – j0,06 ) + ( - 110 + j192 ) ∙ ( 0,07 – j0,07 ) =

0,1 - j0,1 + 0,08 – j0,06 + 0,07 – j0,07 + 0,2 – j0,4

= 15,7 + j0,6 ≈ 15,7 в.

Находим токи в ветвях (линейные токи):

İ_А = (Ė_А - Ů₀ ) Y′ _А = ( 220 – 15,7) ( 0,1 – j0,1 ) = ( 20, 43 – j20,43 ) а;

İ_В = (Ė_В – Ů₀ ) Y′ _В = ( - 110 – j192 – 15,7) ( 0,08 – j0,06 ) = (- 21,5 – j7,8 ) а;

İ_С = (Ė_С – Ů₀ ) Y′ _С = ( - 110 – j192 – 15,7) ( 0,07 – j0,07 ) = (- 21,13 + j4,67 ) а,

то есть

I_А = √ 20,43² + 20,43² = 28,6 а ; I_В = √21,5² + 7,8² = 22,9; I_С = √22,13² + 4,67² = 22,6 а

Определяем напряжение на фазах:

Ů_А = İ_АZ_А = (20,43 – j20,43) ( 3+ j4) = ( 143 + 20,4 ) в;

Ů_В = İ_ВZ_В = ( - 21,5 – j7,8 ) ( 6 + j5 ) = ( -89,8 – j154,3 ) в;

Ů_С = İ_СZ_С = ( - 22,13 – j4,67 ) ( 5 + j6 ) = ( -139,2 – j109,5) в,

или

U_А = √143² + 20,41² ≈ 144 в; U_В = √89,8² + 154,3² = 178 в; U_С = √139,2² + 109,5² = 177в

По полученным данным можно найти все остальные величины (мощности, линейные напряжения на нагрузке, падение напряжения в линии и т.п.).

Нагрузку, работающую без нулевого провода, рассчитываю так же, но в знаменателе уравнения U₀ отсутствует слагаемое Y₀ (Y₀ = 0):

Ů₀ = Ė_А Y′ _А + Ė_В Y′ _В + Ė_С Y′ _С

Y′ _А + Y′ _В + Y′ _С

Часто приходится определять линейные токи и другие параметры нагрузки, когда заданы сопротивления ее фаз и линейное напряжение в сети, к которой подсоединена нагрузка. При этом сопротивления проводов могут быть заданы, а могут быть неизвестны. В этом случае заданное линейное напряжение считают линейным напряжением воображаемого генератора, соединенного звездой, с внутренним сопротивлением, равным нулю,

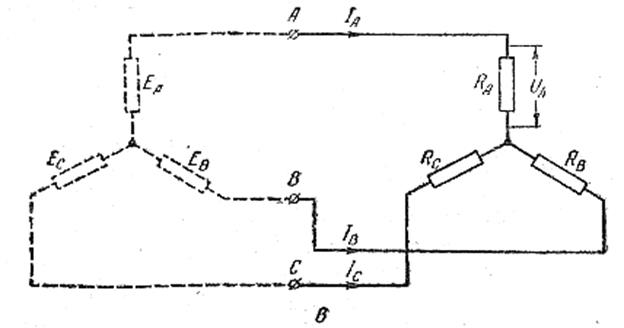
и расчет опять ведут по методу узлового напряжения. При этом в качестве фазных э.д.с. используют фазные напряжения, подсчитанные по заданному линейному.

Пример. Три активных сопротивления R_А, R_В,, R_Ссоединены звездой без нулевого провода и подсоединены к щиту, линейное напряжение на зажимах А, В и С которого 380 в. Определить напряжения на фазах и линейные токи этой нагрузки, если R_А = 20 ом; R_В = 20 ом; R_С = 5 ом.

Решение. Считаем зажимы А, В и С зажимами генератора, соединенного звездой,

тогда Е_А = Е_В = Е_С = 380 = 220 в

√3

Ė_А = 220 в, Ė_В = 220е^-j120о = ( -110 – j192 ) в; Ė_С = 220е^-j120о = (-110 – j192 ) в

Так как нагрузка чисто активная, то

Z_А = R_А + j0 = 20 + j0 = 20 ом, Z_В = 10 ом, Z_С = 5 ом.

Сопротивление подводящих проводов не заданы, значит, ими можно пренебречь, внутреннего сопротивления у воображаемого генератора нет, поэтому

Y_А = _1_ = _1_ = 0,05 сим; Y_В = _1_ = _1_ = 0,1 сим; Y_С = _1_ = _1_ = 0,2 сим

Z_А 20 Z_В 10 Z_С 5

Так как нагрузка работает без нулевого провода, то Z₀ = ∞ и Y₀ = 0.

Тогда

Ů₀ = Ė_А Y_А + Ė_В Y_В + Ė_С Y_С =

Y_А + Y_В + Y_С

= 220 ∙ 0,05 + ( - 110 - j192 ) 0,1 + ( - 110 + j192 ) 0,2 = (-62,8 + j54,8) в.

0,05 + 0,1 + 0,2

Линейные токи

İ_А = (Ė_А - Ů₀ ) Y_А = ( 220 + 62,8 - j54,8) 0,05 = ( 14,1 – j2,74) а;

İ_В = (Ė_В - Ů₀ ) Y_В = (- 110 - j192 + 62,8 - j54,8) 0,1 = (- 4,72 - j24,68 ) а;

İ_С = (Ė_С - Ů₀ ) Y_С = (- 110 - j192 + 62,8 - j54,8) 0,1 = (- 4,72 + j27,4 ) а;

или

İ_А = √14,1² + 2,74² = 14,2 а; İ_В = √4,72² + 24,68² = 25,1 а; İ_С = √9,44² + 27,4² = 29 а.

На основании формулы,

Ů_А = Ė_А - Ů₀;

Ů_В = Ė_В - Ů₀;

Ů_С = Ė_С - Ů_0.

Ů_А = Ė_А - Ů₀ = 220 + 62,8 - j54,8 = ( 282,8 - j54,8 ) в;

Ů_В = Ė_В - Ů₀ = (-110 - j192 ) + 62,8 - j54,8 = (-47,2 – j246,8 ) в;

Ů_С = Ė_С - Ů₀ = (-110 + j192 ) + 62,8 - j54,8 = (-47,2 + j137,2 ) в,

или

U_А = √282,2² + 54,8² = 288 в; U_В = √47,2² + 246,8² = 252 в; U_С= √47² + 137,2² = 145 в.

Из этого примера видно, насколько велика роль смещения нейтрали и насколько несимметричными могут быть из-за этого фазные напряжения.

Все варианты симметричной нагрузки, соединенной звездой, можно рассчитывать тоже по методу узлового напряжения, но при симметричной нагрузке смещение нейтрали отсутствует (U₀ =0 ), поэтому все фазные напряжения равны друг другу и

І_л = І_ф = U_ф = U_{л___},

z √3 z

где z – сопротивление одной фазы нагрузки.

При этом если сопротивления фазных проводов и внутренние сопротивления генератора надо учитывать, то их надо «внести» в сопротивление фаз нагрузки и

І_л = U_{л___},

√3 z′

Соединение треугольником. При соединении неравномерной нагрузки треугольником

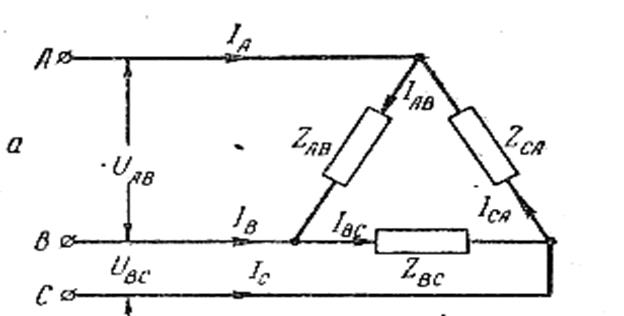
явлений, подобных смещению нейтрали и перекосу фазных напряжений, не наблюдается, но неравномерная нагрузка фаз вызывает неравенство линейных токов и неодинаково нагружает фазы генератора. Из-за этого падения напряжения в отдельных проводах и на внутренних сопротивлениях фаз генератора несколько отличаются друг от друга, поэтому и фазные напряжения оказываются неодинаковыми. Но это неравенство незначительно и при правильном выборе проводов оно настолько мало, что им пренебрегают и считают, что неравномерность нагрузки на фазных напряжениях не отражается.

Расчет нагрузки, соединенной треугольником. При этом следует рассмотреть два основных случая: а) сопротивлением подводящих проводов и внутренним сопротивлением генератора можно пренебречь; б) указанными сопротивлениями пренебрегать нельзя.

Когда сопротивлением фазных проводов и внутренним сопротивлением генератора можно пренебречь, напряжения на фазах нагрузки равны линейному напряжению генератора или сети, к которой эта нагрузка присоединяется, поэтому по заданному линейному напряжению и сопротивлению фаз нагрузки определяют фазные токи, а по ним и линейные токи как геометрические разности соответствующих фазных.

Пример. Определить линейные токи и активную мощность нагрузки, присоединенной к сети с линейным напряжением 380 в, если сопротивления ее фаз Z_АВ = ( 3 + j4 ) ом; Z_ВС = ( 16 + j12 ) ом; Z_СА = ( 7 + j7 ) ом.

Решение. Направим вектор линейного напряжения U_АВ по действительной оси, тогда Ů_АВ = 380 в;

Ů_АВ = 380 е^{- j120о} = 380 ( - 0,5 – j0,87 ) = ( - 190 – j331 ) в;

Ů_АВ = 380 е ^j120о = ( - 190 – j331 ) в.

Сопротивления фаз в показательной форме

Z_АВ = 3 + j4 ≈ 5е ^{j 53о} ом; Z_ВС ≈ 20е ^{j 37о} ом; Z_СА ≈ 10е ^{j 45о} ом.

Фазные токи

İ_АВ = Ů_АВ = 380 = 76е ^{- j 53о} = ( 45,7 – j60,9 ) а;

Z_АВ 5_е^{j 53о}

İ_ВС= Ů_ВС = 380е ^{– j120о} = 19е^{- j157о} = ( - 17,5 – j 7,4 ) а;

Z_ВС 20е ^{j 37о}

İ_СА= Ů_СА = 380е ^j120о = 38 е ^j75о = ( 9,81 + j36,3 ) а.

Z_ВС 10 е ^{j 45о}

Так как фазные токи неодинаковы, то линейные приходится находить, как разность соответствующих фазных:

İ_А = İ_АВ - İ_СА = 45, 7 – j60,9 – 9,81 – j36,3 = (35,89 – j97,2 ) а;

İ_В = İ_ВС - İ_АВ = - 17,5 – j7,4 – 45,7 + j60,9 = ( - 63,20 + j53,5 ) а;

İ_С = İ_СА – İ_ВС = 9,81 + j36,3 + 17,5 + j7,4 = ( 27,31 + j43,7 ) а.

или

І_А = √ 35,89² + 97,2² = 103,8 а; І_В = √ 63,30² + 53,5² = 82,8 а;

І_С = √ 27,31² + 43,7² = 51,6 а.

Фазные мощности:

Š_АВ = Ů_АВ Ĩ_АВ = 380 ( 45,7 + j60,9 ) = ( 17 400 + j23 150 ) ва;

Š_ВС = Ů_ВС Ĩ_ВС = ( - 190 + j7,4 ) = ( 5780 + j4390 ) ва;

Š_СА = Ů_СА Ĩ_СА = ( - 190 + j331 ) ( 9,81 – j36,3 ) = ( 10 180 + j10 145 ) ва.

Активная мощность всей цепи

Р = Р_АВ + Р_ВС + Р_СА = 17 400 + 5780 + 10 180 = 33 360 вт.

Если нагрузка симметрична, то фазные токи одинаковы, расчет значительно упрощается и его можно провести без использования комплексных чисел.

І_Ф = U_л ; І_л = І_Ф √ 3, а Р = √ 3 U_л І_л cos φ.

z

Если сопротивлениями подводящих проводов или внутренним сопротивлением фаз генератора пренебречь нельзя,

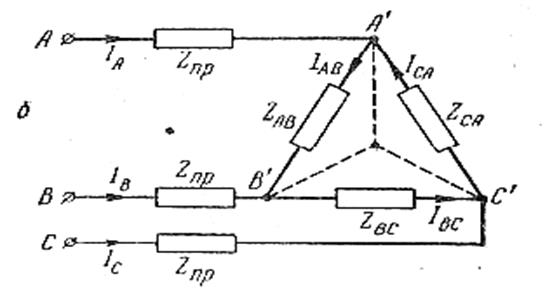
То сопротивления проводов Z_пр и внутреннее сопротивление фаз генератора (если оно задано) надо «внести» в фазы нагрузки, а для этого треугольник следует заменить эквивалентной звездой и «вносить» их уже в фазы звезды. Затем решать цепь так, как ее решают при соединении нагрузки звездой.

Пример. Определить линейные токи нагрузки, изображенной на рисунке, если она питается от сети с U_л = 380 в, причем

Ż_АВ = ( 7 + j7 ) ом, Ż_ВС = 10 ом; Ż_СА = 20 ом; Ż_пр = 2 ом.

Решение. Треугольник А΄В΄С΄ преобразуем в эквивалентную звезду

Z_А = __ Z_АВ Z_СА____ = _( 7 + j7 )· 20_ = ( 7 + j7 )· 20 = ( 4,73 + j3,35 ) ом;

Z_АВ + Z_ВС + Z_СА 7 + j7 + 10 + 20 37 + j7

Z_В = __ Z_АВ Z_ВС____ = _( 7 + j7 )· 10 = (2,365 + j1,675 ) ом;

37 + j7 37 + j7

Z_С = __ Z_СА Z_ВС____ = 20 · 10_ = ( 5,2 - j 0,982 ) ом.

37 + j7 37 + j7

Внесем сопротивления проводов в фазы звезды:

Z΄_А = Z_А + Z_пр = 4,73 + j3,35 + 2 = ( 6,73 + j3,35 ) ом;

Z΄_В = Z_В + Z_пр = 2,365 + j1,675 + 2 = ( 4,365 + j1,675 ) ом;

Z΄_С = Z_С + Z_пр = 5,2 – j0,982 + 2 = ( 7,2 – j0,982 ) ом.

Э. д. с. воображаемого генератора Е_Ф = 380 = 220 в

√ 3

Направим Ē_А по действительной оси, тогда Ė_А = 220 в. Ė_В = 220е ^{– j120о} =

= ( - 110 – j192 ) в; Ė_С = 220е ^j120о = ( - 110 + j192 ) в.

Проводимость ветвей:

Y΄_А = _1_ = ____1_____ = ( 0,119 - j0, 059 ) сим;

Z΄_А 6,73 + j3,35

Y΄_В = _1_ = ____1_______ = ( 0,2 - j0,0765 ) сим;

Z΄_В 4,365 + j1,675

Y΄_С = _1_ = ____1_______ = ( 0,1795 + j0,0338 ) сим.

Z΄_С 5,2 – j0,982

Узловое напряжение

Ů₀ = Ė_А Y΄_А + Ė_В Y΄_В + Ė_С Y΄_С =

Y΄_А + Y΄_В + Y΄_С

= 220 (0,119 – j0,059) + (-110 – j192) (0,2 – j0,0765) + (-110 + j192) (0,1795 + j0,0338)=

0,119 – j0,059 + 0,2 – j0,0765 + 0,1795 + j0,0338

= ( -21,2 – j64,3 )в.

Линейные токи:

İ_А = (Ė_А - Ů₀ ) Y΄_А = ( 220 + 21,2 + j64,3 ) (0,119 – j0,059 ) = ( 33,5 – j6,6 )а;

İ_В = (Ė_В - Ů₀ ) Y΄_В = (- 110 – j192 + 21,2 + j64,3 ) ( 0,2 – j0,0765) = (-27,6 – j 18,7 ) а;

İ_С = (Ė_С - Ů₀ ) Y΄_С = (-110 + j192 + 21,2 + j64,3 ) ( 0,1795 + j0,0338) = (-26,67 + j43 )а.

или

I_А = √ 33,5² + 6,6² = 34,2 а; I_В = √ 27,6² + 18,7² = 33,3 а; I_С = √ 24,67² + 43² = 50,6 а.

Если нагрузка будет симметричной, то решение будет отличаться тем, что после преобразования треугольника в звезду и «внесения» в нее сопротивлений проводов, нет надобности заканчивать решение методом узлового напряжения, так как звезда будет симметричной, напряжения на ее фазах будут одинаковые и их можно подсчитать по заданным линейным напряжениям.