Симметричные составляющие несимметричной системы.


Всякую несимметричную систему трех вращающихся векторов можно рассматривать состоящий из трех симметричных систем:

1) симметричной системы трех вращающихся векторов прямой последовательности;

2) симметричной системы трех вращающихся векторов обратной последовательности;

3) симметричной системы трех вращающихся векторов нулевой последовательности.

Системой нулевой последовательности называют систему трех вращающихся вектров, совпадающих друг с другом по фазе.

На рисунке изображена заданная несимметричная система, состоящая из трех векторов А, В, и С, и ее симметричные составляющие.

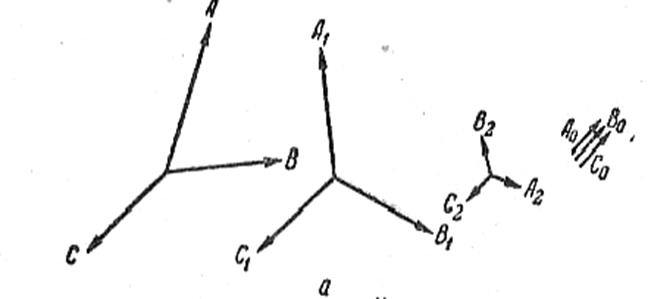
Составляющие прямой последовательности принято отмечать индексом 1, обратной – индексом 2 и нулевой – индексом 0.

Симметричная система А1В1С1 имеет прямую последовательность, так как в ней за вектором А идет вектор В, а затем вектор С (векторы вращаются против часовой стрелки), то есть в том порядке, что и в заданной несимметричной системе.

Симметричная система А2В2С2 – обратной последовательности, так как в ней за вектором а идет вектор С, а не В. Система А0В0С0 – нулевой последовательности, у нее все три вектора по фазе друг с другом совпадают.

Если все эти три симметричные системы сложить, то получится заданная несимметричная система, причем

А' = А'1 + А'2 + А'0; В '= В '1 + В '2 + В '0; С ' = С '1 + С '2 + С '0.

Разложить несимметричную систему на симметричные составляющие – это значит определить векторы симметричных систем, то есть определить их величины и направления, причем так как искомые системы симметричны, то нет необходимости определять девять векторов. Достаточно определить по одному вектору из каждой системы ( например, А'1, А'2 и А'0), а остальные будут такими же, но только повернуты относительно А'1 и А'2 на 120о. легче всего найти Ã1, Ã2и Ã0, а комплексы отражают величины векторов и их направления. При этом несимметричная система должна быть задана комплексами А˚, В˚ и С˚, таким образом, задача сводится к нахождению А'1, А'2 и А'0 по заданным А˚, В˚ и С˚.

Представим себе, что разложение уже произведено и симметричные системы, изображенные на рисунке, являются составляющими заданной несимметричной системы, состоящей из А', В ' и С '. Тогда

А˚ = А˚0 + А˚1 + А˚2;

В˚ = В˚0 + В˚1 + В˚2;

С˚ = С˚0 + С˚1 + С˚2.

Для краткости будем считать, что е – j120о = С˚а. умножение вектора на такой поворотный множитель означает поворот его в положительную сторону на 120 о. Так как поворот в отрицательную сторону на 120о равносилен двукратному повороту вперед на 120о, то

е – j120о = е j 240о = е j 120о · е j 120о = а2.

Умножение вектора на а3 означает трехкратный поворот вектора на 120о, отчего вектор становится в свое исходное положение, поэтому а3 = 1 и а4 = а3а = а.

Так как сумма трех одинаковых векторов, сдвинуты по фазе на 120о, равна нулю, то 1 + 1а + 1а2 = 0.

В уравнениях

А˚ = А˚0 + А˚1 + А˚2;

В˚ = В˚0 + В˚1 + В˚2;

С˚ = С˚0 + С˚1 + С˚2.

В˚1 = а2 А˚1; С˚1 = а А˚1; В˚2 = а А˚2 ; С˚2 = а2 А˚2; А˚0 = В˚0 = С˚0

В связи с этим

А˚ = А˚0 + А˚1 + А˚2;

В˚ = А˚0 + а2 А˚1 + а А˚2;

С˚ = А˚0 + аА˚1 + а2 А˚2.

Сложив эти уравнения, получим:

А˚ + В˚ + С˚ = А˚0 + А˚1 + А˚2 + А˚0 + а2 А˚1 + а А˚2 + А˚0 + аА˚1 + а2 А˚2 =

= 3 А˚0 + А˚1 ( 1 + а2 + а ) + А˚2 ( 1 + а + а2 ) = 3 А˚0,

откуда

А˚0 = А˚ + В˚ + С˚

Умножим В˚ = А˚0 + а2 А˚1 + а А˚2 на а, а уравнение С˚ = А˚0 + аА˚1 + а2 А˚2 на а2, тогда система уравнений примет вид:

А˚ = А˚0 + А˚1 + А˚2; аВ˚ = аА˚0 + А˚1 + а2А˚2; а2С˚ = а2А˚0 + А˚1 + аА˚2.

Складывая уравнения почленно, получим:

А˚ + аВ˚ + а2С˚ = А˚0 (1 + а + а2) + 3 А˚1 + А˚2 (1 + а2 + а ) = 3А1.

Откуда

А˚1 = А˚ + аВ˚ + а2С˚.

Умножим уравнение В˚ = В˚0 + В˚1 + В˚2 на а2, а уравнение С˚ = С˚0 + С˚1 + С˚2 на а.

Тогда

А˚ = А˚0 + А˚1 + А˚2; а2В˚ = а2А˚0 + аА˚1 + А˚2; аС˚ = аА˚0 + а2А˚1 + А˚2.

Складывая их почленно, получим:

А˚ + а2В˚ + аС˚ = А˚0 (1 + а2 + а ) + А1 ( 1 + а + а2 ) + 3 А˚2 = 3 А˚2.

Откуда

А˚2 = А˚ + а2В˚ + аС .

По этим уравнениям и определяют симметричные составляющие заданной несимметричной системы.

Если задана несимметричная система линейных напряжений,

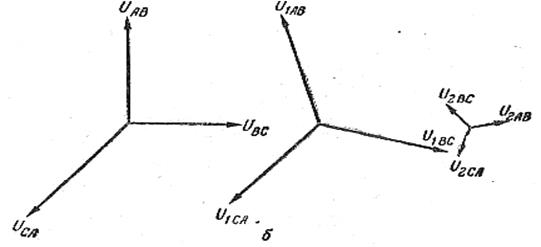
то

ŮАВо = ŮАВ + ŮВС + ŮСА = 0,

так как

ŮАВ + ŪВС + ŪСА = 0,

То есть в линейныхнапряжениях всегда отсутствует составляющая нулевой последовательности и всякая несимметричная система линейных напряжений состоит только из систем прямой и обратной последовательности, причем чем более несимметрична система линейных напряжений, тем больше величина векторов обратной последовательности, и наоборот. Если несимметричная система линейных напряжений станет симметричной, то векторы обратной последовательности при этом станут равными нулю и теперь уже ставшая симметричной система линейных напряжений будет состоять только из одной системы прямой последовательности, то есть из самой себя. В связи с этим по величине векторов обратной последовательности можно судить о степени несимметричности линейных напряжений, и отношение модуля векторов обратной последовательности к модулю векторов прямой последовательности, выраженное в процентах, называют степенью асимметрии (несимметрии) и обозначают буквой α:

Α = U2 100%

U1

По нормам степень ассиметрии линейных напряжений не должна превышать 5 %.

Пример. Определить степень ассиметрии линейных напряжений, если они выражаются следующими комплексами:

ŮАВ = 220е j90о = j220 в; ŮВС = 220 в; ŮСА = 298- j 135о = (- 200 – j200) в.

Составляющая нулевой последовательности UАВ0 = 0.

Составляющая прямой последовательности

ŮАВ1 = ŮАВ + а ŮВС + а2 ŮСА = j220 + е j 120о200 + е- j120о298е- 135о =

3 3

= j220 + (-0,5 + j0,87 )200 + (-0,5 – j0,87) (-200 - j220) = (-67 + j226) в.

Составляющая обратной последовательности

ŮАВ2 = ŮАВ + а2 ŮВС + а ŮСА =

= j220 + (- 0,5 – j0,87) 200 + (-0,5 + j0,87) (-200 – j220) = (60,5 – j6 ) в

Чтобы построить систему прямой последовательности, задается масштабом и строим ŮАВ1 в соответствии с его комплексом. К его началу пристраиваем еще два таких же вектора, повернутых относительно ŮАВ1 вправо и влево на углы по 120о.

Точно так же и в том же масштабе строим систему обратной последовательности. Если обе симметричные системы сложить, то получится заданная система линейных напряжений, изображенная слева.

Модуль векторов прямой последовательности

ŮАВ1 = √ 672 + 2262 = 235 в.

Модуль векторов обратной последовательности

ŮАВ2 = √ 60,52 + 62 = 60,8 в.

Степень ассиметрии

Α = ŮАВ2 100 = 60,8 100 = 25,9%

ŮАВ1 235

В сетях такую несимметричность линейных напряжений допускать нельзя. Надо найти причину ассиметрии и устранить ее. Можно считать, что в сети с такими линейными напряжениями действуют два напряжения: 235 в – прямой последовательности и 60,8 в – обратной последовательности. Если в нее включить, например, трехфазный двигатель, то напряжение в 235 в прямой последовательности будет создавать в нем вращающий момент, а напряжение в

60,8 в – обратной последовательности. Будет создавать хотя и меньший вращающий момент, но направленный в обратную сторону, и нормальная работа машины будет нарушена. Поэтому не допускают, чтобы составляющая обратной последовательности превышала 5% составляющей прямой последовательности (чтобы ее роль не была значительной).

Кроме того, прием разложения несимметричной системы векторов на симметричные составляющие используется для анализа режимов в трехфазных цепях при однофазных и двухфазных коротких замыканиях, при обрывах в линиях.


Дата добавления: 2020-03-17; просмотров: 643;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.015 сек.