Информационное моделирование источников визуальных сообщений и фотоизображений
Цель работы. Изучение методов информационной оценки качества источников визуальных сообщений и фотоизображений, используемых в системах автоматической обработки изображений.
Теоретическое обоснование. Качество считанных цифровых изображений в огромной степени зависит от качества исходных изображений, которое может характеризоваться их информационными емкостями, т.е. максимальным количеством информации приходящиеся на единицу их площади. Поэтому, исходя из информационных моделей, необходимо рассчитать информационные характеристики
- исходного оптического изображения ;
- фотоизображения.
1. Информационные характеристики оптического изображения, как функция линейного размера (d) элемента разложения, определяются из следующих соотношений:
- число различимых уровней контраста (m):
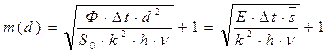 ;
;
- среднее максимальное количество информации приходящееся на один элемент разложения h(d):
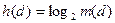 (бит/символ);
(бит/символ);
- предельное количество информации I(d), содержащееся во всем изображении площадью S:
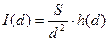 (бит);
(бит);
- информационная емкость изображения (предельное количество информации, содержащееся в изображении единичной площади) H(d)
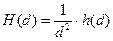 (бит/ед. площади),
(бит/ед. площади),
где Ф - световой поток падающий на изображение;
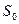 - площадь изображения;
- площадь изображения;
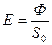 - освещенность изображения;
- освещенность изображения;
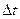 - время экспозиции;
- время экспозиции;
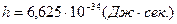 - постоянная Планка;
- постоянная Планка;
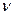 - частота падающего монохроматического света;
- частота падающего монохроматического света;
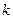 - кратность превышения минимально различимым контрастом среднеквадратического уровня шума, вызванного флуктуацией потока падающих фотонов, которая находится из Таблицы 1
- кратность превышения минимально различимым контрастом среднеквадратического уровня шума, вызванного флуктуацией потока падающих фотонов, которая находится из Таблицы 1
Таблица 1
| k | |||||
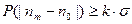
| 0,32 | 0,046 | 0,00027 | 0,000063 | 0,00000057 |
2. Характерной особенностью фотоизображения является наличие на них шумов, вызванного их зернистостью фотослоя, которые ведут к флуктуациям оптической плотности, среднеквадратическое значение которой ( 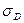 ) определяется выражением:
) определяется выражением:
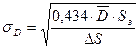 ,
,
где 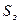 - средняя площадь проекции одного зерна фотослоя, зависящая от типа фотоносителя;
- средняя площадь проекции одного зерна фотослоя, зависящая от типа фотоносителя;
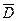 - средняя оптическая плотность фотоизображения;
- средняя оптическая плотность фотоизображения;
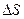 - площадь элементарного участка фотоизображения.
- площадь элементарного участка фотоизображения.
Отношение сигнал \ шум фотоизображения ( 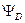 ) определяется соотношением:
) определяется соотношением:
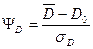 ,
,
где 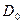 - плотность вуали.
- плотность вуали.
Предельное количество информации, содержащееся в фотоизображении единичной площади (т.е. информационная емкость фотоизображения) 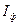 можно найти из выражения:
можно найти из выражения:
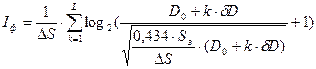 (бит/ед.площади),
(бит/ед.площади),
где 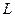 - число равноотстоящих уровней плотности;
- число равноотстоящих уровней плотности;
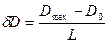 - величина разности между соседними уровнями.
- величина разности между соседними уровнями.
Количество информации, содержащееся в одной элементарной площадке фотоизображения, определяется выражением:
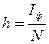 (бит),
(бит),
где 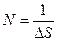 .
.
Выполнение работы:
1.Определить информационные характеристики оптического изображения размером S=0,2*0,2 м2 при его равномерной освещенности гелий-неоновым лазером мощностью Ф и длиной волны света 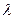 =0,63 мкм.(
=0,63 мкм.( 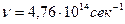 ). Считывание производится квадратной аппертурой с линейным размером
). Считывание производится квадратной аппертурой с линейным размером 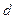 (
( 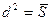 ) с быстродействием
) с быстродействием 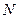 элементов/сек. (
элементов/сек. ( 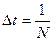 ) и допустимой погрешностью измерения различных уровней контраста не превышающей
) и допустимой погрешностью измерения различных уровней контраста не превышающей 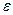 . Значения Ф,
. Значения Ф, 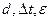 взять из Таблицы 2 в соответствии с заданным вариантом.
взять из Таблицы 2 в соответствии с заданным вариантом.
Построить графики зависимостей: 
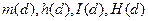 при
при 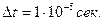
Найти и распечатать значения этих характеристик при 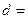 2, 5, 10, 15, 25 мкм.
2, 5, 10, 15, 25 мкм.
Построить графики зависимостей: 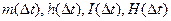 при
при 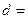 10 мкм.
10 мкм.
Найти и распечатать значения этих характеристик при 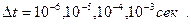
Проанализировать полученные результаты.
2.Произвести анализ выражения для определения информационной емкости фотоизображения на примере фотоизображения площадью 1 мм2 при Dmax=2,7; D0=0,1; Sз= 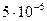 мм2; d=
мм2; d= 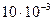 мм. При этих значениях параметров найти значение
мм. При этих значениях параметров найти значение 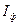 при L=2n (n=1, 2,….8).
при L=2n (n=1, 2,….8).
Построить графики информационных характеристик 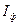 и
и 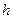 от линейного размера элементарной площадки
от линейного размера элементарной площадки 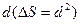 при значении L=64.
при значении L=64.
Найти и распечатать значения этих характеристик при d=2, 5, 10, 15, 25 мкм.
3.Сравнить полученные результаты с п.1, т. е. определить относительные потери информации, содержащейся в оптическом изображении, при регистрации его на фотоносителе при заданном d. Для этого вычислить коэффициент 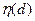 при
при 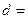 2, 5, 10, 15, 25 мкм.
2, 5, 10, 15, 25 мкм.
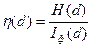 .
.
Таблица 2.
| № | |||||||||||||
| Ф(вт.) | |||||||||||||
| d(мкм) | |||||||||||||
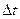 (сек.) (сек.)
| 10-6 | 10-5 | 10-4 | 10-6 | 10-5 | 10-4 | 10-6 | 10-5 | 10-4 | 10-3 | 10-6 | 10-5 | 10-4 |
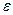
| 0,01 | 0,01 | 0,1 | 0,1 | 0,01 | 0,01 | 0,1 | 0,1 | 0,01 | 0,01 | 0,1 | 0,1 | 0,01 |
Контрольные вопросы.
- Что такое информационное моделирование?
- Общий вид информационной модели и её составляющие.
- Дайте определение пространственного разрешения и разрешения по плотности.
- Информационные характеристики оптического изображения.
- От каких основных параметров зависит информационная ёмкость оптического изображения.
- Что является причиной появления шумов фотоизображения, как они проявляются и от каких параметров зависят.
- От каких основных параметров зависит информационная ёмкость фотоизображения.
Приложение.
Некоторые полезные сведения из теории вероятностей.
Случайные события.
1.1. Событием (U) называют всякий факт, который может произойти или не произойти.
1.2. Вероятностью события P(U) называется численная мера степени объективной возможности этого события.
1.3. Достоверным событием называют событие (U), которое в результате опыта непременно должно произойти. Вероятность достоверного события принимается равной единице, т.е. P(U)=1.
1.4 Невозможным событием называют событие Q, которое в результате опыта никоим образом не может произойти. Вероятность невозможного события принимается равной нулю, т.е. P(Q)=0.
1.5 Из п.1.3. и 1.4. следует, что вероятность любого реального события (А) заключена в интервале от 0 до 1, т.е. 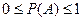 .
.
1.6 Несколько событий в данном опыте называют несовместными, если никакие два из них не могут произойти одновременно.
1.7.Несколько событий в данном опыте называют равновозможными, если по условиям симметрии опыта нет оснований считать какое-либо из них более предпочтительным или возможным.
1.8.Условной вероятность события А при наличии события В называют вероятность события А, вычисленную при условии, что событие В произошло. Условная вероятность в этом случае обозначается как Р(А/В).
1.9.События называются независимыми, если появление одного из них никоим образом не меняет вероятности появления другого. Для независимых событий А и В справедливо:
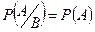 ,
, 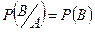 .
.
1.10 . Полной группой событий называют несколько событий таких, что в результате опыта непременно произойдет хотя бы одно из них. Если события Аk (k=1, 2, …,n) составляют полную группу событий и несовместны, то
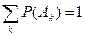 ,
,
так как 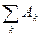 - достоверное событие.
- достоверное событие.
1.11. Если несколько событий
а) образуют полную группу событий;
б) несовместны;
в) равновозможны,
то вероятность события А можно вычислить по формуле
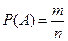 ,
,
где n – общее число возможных событий (исходов опыта),
m – число событий, благоприятствующих событию А.
Алгебра событий
2.1. Случайные события обозначают большими буквами алфавита.
2.2. Равенство двух событий А и В (А=В) означает, что появление одного события непременно влечет за собой появление другого.
2.3. Суммой двух событий А и В называют событие С (С=А=В), заключающееся в появлении хотя бы одного из событий А и B.
2.4. Произведением двух событий А и В называют событие С(С=А·В), заключающееся в одновременном наступлении обоих событий А и В.
2.5. Если результат какого- либо опыта может иметь два взаимно исключающих события А и В (полная группа событий), одно из этих событий называют противоположным событием другому, например, событие В - противоположное событию А и обозначается Ă (читается как «не А»). Для прямого события А и противоположного события Ă (как составляющих полную группу событий) справедливо тождество:
Р(А) + Р(Ă)=1.
2.6. Теорема сложения вероятностей. Вероятность суммы двух событий А и В равна сумме вероятностей этих событий без вероятности произведения этих событий, т.е.
Р(А+В)=Р(А) + Р(В)- Р(А·В).
В случае, если А и В несовместны, то Р(А·В)=0 и, следовательно,
Р(А+В)=Р(А)+Р(В).
2.7.Теорема умножения вероятностей. Вероятность произведения двух событий А и В равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого, т.е.
Р(А·В) = Р(А·В) = Р(А)·Р(В/А) = Р(В)·Р(А/В).
В случае, если события А и В независимы, то с учетом п.1.9 справедливо:
Р(А·В)=Р(А)·Р(В)= Р(В)·Р(А).
2.8. Полезное правило решения задач на нахождение вероятности случайных событий.
Для того, чтобы найти вероятность интересующего события, необходимо:
а) с помощью алгебры событий описать интересующее событие через известные события, т.е. через такие события, вероятности которых известны;
б) с помощью теорем вероятности суммы и вероятности произведения найти вероятность интересующего события.
Дата добавления: 2018-11-26; просмотров: 907;











