Статистические характеристики случайных величин.

4.1. Математическое ожидание случайной величины X (обозначают M[X] или m_x) – это среднее значение случайной величины, вычисленное по формулам:

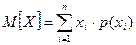- для дискретных случайных величин;

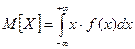- для непрерывных случайных величин.

4.2. Центрированной случайной величиной ºX называют разность между самой случайной величиной X и ее математическим ожиданием M[X], т.е.

ºX = X - M[X].

4.3. Дисперсия случайной величины X (обозначается D[X] или d_x) ― это есть математическое ожидание квадрата соответствующей ей центрированной случайной величины, т.е.

D[X]=M[ºX²],

которая вычисляется по формулам:

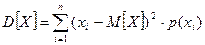- для дискретных случайных величин;

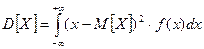- для непрерывных случайных величин.

Дисперсия характеризует среднее отклонение значений случайной величины от её математического ожидания. Размерность дисперсии не совпадает с размерностью характеризуемой случайной величины. Размерность дисперсии есть квадрат размерности соответствующей случайной величины.

4.4. Среднее квадратическое отклонение (σ_ч) случайной величины X―это есть квадратный корень из ее дисперсии, т.е.

.

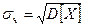Среднее квадратическое отклонение иногда называют стандартом. Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.

4.5. Начальным моментом порядка k (ν_k) случайной величины X называют математическое ожидание k-той степени этой случайной величины, т.е.

.

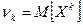4.6. Центральным моментом порядка k (μ_k) случайной величины X называют математическое ожидание k-той степени отклонения этой случайной величины от ее математического ожидания, т.е.

4.7. Эксцесс случайной величины (Е) – это есть величина, вычисленная по формуле:

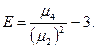
Для нормального закона распределения Е=0, отличие эксцесса от нуля указывает на отклонение эмпирического закона распределения от нормального закона распределения.

4.8. Ассиметрия характеризует симметричность кривой распределения случайной величины X. Показатель ассиметрии (S) вычисляется по формуле:

.

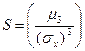Для симметричных распределений S=0.

Случайные функции.

5.1. Случайной функцией X(t) называют функцию, которая в результате опыта может принимать тот или иной конкретный вид, неизвестный заранее.

5.2. Конкретный вид, принимаемый случайной функцией, называют реализацией случайной функции.

5.3. Сечением случайной функции называют случайную величину X(t_k), в которую обращается случайная функция X(t) при фиксированном аргументе (t = t_k).

5.4. Одномерным законом распределения случайной функции X(t) называют закон распределения f(x,t_k) сечения X(t) случайной функции.

5.5. Математическим ожиданием случайной функции X(t) называют неслучайную функцию m_x(t), которая при каждом значении аргумента t представляет собой математическое ожидание соответствующего сечения этой случайной функции.

5.6. Дисперсией случайной функции X(t) называют неслучайную функцию d_x(t), которая при каждом значении аргумента t представляет собой дисперсию соответствующего сечения этой случайной функции.

5.7. Корреляционной функцией случайной функции X(t) называют неслучайную функцию двух аргументов R_x(t_k,t₁), которая при каждой паре значений аргументов t_k и t₁ равна корреляционному моменту соответствующих сечений случайной функции, т. е.

,

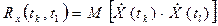где 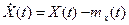- центрированная случайная функция.

Корреляционная функция характеризует статистическую связь между сечениями случайной функции, т.е. внутреннюю структуру случайной функции. При t_k = t₁ корреляционная функция обращается в дисперсию, действительно,

.

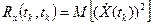5.8. Нормированной корреляционной функцией случайной функции X(t) называют неслучайную функцию двух аргументов r_x(t_k,t_k1), определяемую по формуле:

,

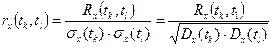при t_k = t₁ r_x(t_k ,t_k1) = 1.

5.9. Стационарной случайной функцией называют случайную функцию, математическое ожидание которой постоянно ( 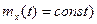, а её корреляционая функция зависит только от разности между аргументами:

,

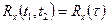где τ = t₁ - t₂.

Литература.

1.Журкин И.Г. Шавенько Н.К Сигналы Учебное пособие по курсу «Автоматизированная обработки аэрокосмической информации. –М.: Изд. МИИГАиК, 2007.

2.Дмитриев В.И. Прикладная теория информации.- М.:Изд.«Высшая школа»,1999г.

3.Хэмминг Р.В. Теория кодирования и теория инфорции.―М.:Изд. «Радио и связь»,1998г.

4.Колесник В.Д., Полтырев Г.Ш. Курс теории информации. -М.: Изд.»Наука», 1994г.

5.Мощиль В.И., Шавенько Н.К. Основы теории информации. Учебное пособие. –М.: Изд. МИИГАиК, 2006.

6. Мощиль В. И., Шавенько Н. К. Основы теории кодирования. Учебное пособие. –М.: Изд. МИИГАиК, 1999.

7. Новиков Ф.А. Дискретная математика для программистов. –Санкт–Петербург; Изд.дом «Питер», 2008.