Балансовые методы и макроэкономическое моделирование
Макроэкономическое прогнозирование предполагает определение прогнозных оценок ряда макроэкономических показателей с целью обоснования перспектив экономического развития государства. К таким показателям можно отнести:
· валовой внутренний продукт (ВВП) – валовая рыночная стоимость товаров и услуг, произведённых на территории страны за определенный период времени (обычно за год). ВВП может быть измерен через национальное производство, доходы и конечное потребление;
· добавленная стоимость – разница между стоимостью произведённых товаров и услуг и стоимостью промежуточного потребления (материальными затратами и амортизационными отчислениями);
· чистый национальный продукт – показатель, характеризующий результат производственной деятельности. Рассчитывается как разность между валовым продуктом и величиной затрат на возмещение износа основного капитала (амортизацией);
· инвестиции – долгосрочные вложения капитала частным сектором и государством внутри страны и за границей в различные отрасли экономики.
· чистый экспорт – превышение экспорта над импортом;
· промежуточное потребление – использование продуктов труда одной стадии производства в качестве предметов труда на другой стадии производства;
· ряд других показателей.
В качестве информационной базы для макроэкономического прогнозирования выступает система национальных счетов.
В прогнозировании развития общегосударственного экономического комплекса в мировой экономической практике большое распространение получил метод межотраслевого баланса (МОБ), разработанный в 30-е гг. американским экономистом В.В. Леонтьевым.
Главное направление МОБ – обосновать рациональный уровень производства на основе показателей конечной продукции и промежуточных затрат. Применение МОБ облегчает вариантные расчёты экономического развития при различных сдвигах в структуре общественного производства.
Метод межотраслевого анализа является универсальным способом ответа на вопросы, связанные с анализом равновесия на национальном рынке. Его использование позволяет увязать макроэкономические показатели, характеризующие развитие национальной экономики с микроэкономическими показателями формирования спроса и предложения на уровне отдельных отраслей или продуктов.
В экономической работе на разных уровнях управления применяются следующие виды МОБ: детальные и агрегированные; статистические и динамические; натуральные, стоимостные и натурально-стоимостные; народнохозяйственные и региональные[3].
Детализированная схема МОБ включает в себя четыре раздела (квадранта) (таблица 3.5).
Таблица 3.5 – Общая схема межотраслевого баланса
| Отрасли – покупатели Отрасли – продавцы | Отрасли производства (сектора) | Конечный спрос (частное потребление, инвестиции, экспорт, импорт, государственные расходы т.д.) | Объём выпуска | |||
| j | n | |||||
| Первый квадрант | Второй квадрант | |||||
| X11 | X12 | X1j | X1n | Y1 | X1 | |
| X21 | X22 | X2j | X2n | Y2 | X2 | |
| i | Xi1 | Xi2 | Xij | Xin | Yi | Xi |
| n | Xn1 | Xn2 | Xnj | Xnn | Yn | Xn |
| Третий квадрант | Четвёртый квадрант | |||||
| Добавленная стоимость (доход занятых по найму, предпринимательская прибыль, амортизационные отчисления, косвен- ные налоги и т.д.) | Z1 | Z2 | Zj | Zn | Перераспределение факторных доходов в элементы конечного спроса | |
| Объём выпуска | X1 | X2 | Xj | Xn |
В первом квадранте отражаются межотраслевые затрат, во втором – отраслевая структура конечного спроса, в третьем – факторные доходы, в четвёртом – трансформация факторных доходов в элементы конечного спроса.
В первом разделе баланса отражаются те потоки продукции, которые идут на текущее потребление в процессе производства. Этот раздел имеет «шахматный вид». Состав отраслей – производителей и отраслей – потребителей одинаковый. В них входят все отрасли производства.
В зависимости от целей построения баланса и имеющейся информации число отраслей может колебаться от нескольких десятков до нескольких сотен. В качестве таковых могут выступать агрегаты как промышленность, транспорт, и вместе с тем отдельные производства: чёрная металлургия, цветная металлургия, машиностроение и т.д. Итог первого квадранта – это общий объём промежуточного потребления текущих материальных затрат. Второй раздел межотраслевого баланса описывает конечный продукт, который расходуется на личное и общественное потребление, на накопление, возмещение выбытия основных фондов, а также включает экспортно-импортное сальдо. Конечный продукт отличается от ВВП на величину текущих материальных затрат, а также на величину экспортно-импортного сальдо.
Второй раздел межотраслевого баланса описывает конечный продукт, который расходуется на личное и общественное потребление, на накопление, возмещение выбытия основных фондов, а также включает экспортно-импортное сальдо.
Конечный продукт отличается от ВВП на величину текущих материальных затрат, а также на величину экспортно-импортного сальдо.
Первый и второй разделы вместе характеризуют распределение продукции и связаны следующим соотношением:
Xi = 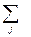 Xij + Yi , (при i = 1,2…,n),
Xij + Yi , (при i = 1,2…,n),
где Xij – количество продукции вида i, израсходованное на производство продукции вида j (например, количество электроэнергии, израсходованное в черной металлургии) в денежном выражении;
Yi – количество продукта i на конечное потребление (например, какое количество продукции машиностроения ушло на конечное потребление, т.е. нам на стол или на накопление) в денежном выражении;
Xi – объём производства продукции i в денежном выражении (т.е. сколько всего продукции произведено в данной отрасли).
Формула говорит о том, что всё произведённое в отрасли i было потрачено либо на промежуточное потребление, либо на конечное.
Первый и третий раздел отражают формирование общественных издержек производства. Они связаны следующим образом: стоимость продукта складывается из материальных затрат и добавленной стоимости, которая включает в себя оплату труда работников, чистую прибыль, налоги и дотации на продукты и т.д. Эта связь отражается соотношением:
Xj = 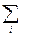 Xij+ Zj, (при j = 1,2…,n),
Xij+ Zj, (при j = 1,2…,n),
где Zj – величина условно-чистой продукции (добавленной стоимости) в стоимости продукта j -го вида.
В четвёртом квадранте закрытой модели межотраслевого баланса отражено перераспределение доходов. Речь идёт о трансформации факторных доходов, отражённых в третьем квадранте, в элементы конечного спроса (представленного во втором квадранте). Для заполнения этой части баланса на будущее необходимо иметь данные о распределении продукции и доходов отдельными агентами воспроизводственной деятельности.
Наиболее распространённой и методически разработанной является статическая модель межотраслевого баланса. Она основана на сочетании балансовых соотношений, характеризующих формирование стоимости валового внутреннего продукта и его распределение по направлениям конечного использования.
Принципиальная схема построения этого баланса – наложение крест-накрест двух таблиц, одна из которых – горизонтальная (включающая первый и второй разделы МОБ) – показывает распределение продукции в народном хозяйстве на промежуточное и конечное потребление, а другая – вертикальная (охватывающая первый и третий разделы МОБ) – характеризует формирование общественных издержек производства (факторных доходов).
Горизонтальная таблица включает в себя n уравнений распределения продукции каждой отрасли на промежуточное и конечное потребление.
Уравнение распределения валовой продукции национальной экономики выглядит следующим образом:
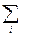 Xi =
Xi = 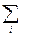
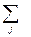 Xij + åYi , (при i = 1,2…,n).
Xij + åYi , (при i = 1,2…,n).
Вертикальная таблица включает n уравнений, описывающих формирование стоимости продукции по отдельным отраслям.
Уравнение формирования стоимости валовой продукции национальной экономики может быть представлено так:
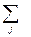 Xj =
Xj = 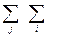 Xij +
Xij + 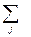 Zj, (при j = 1,2…,n).
Zj, (при j = 1,2…,n).
Основные балансовые равенства статической открытой модели МОБ следующие:
1. 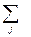 Xj=
Xj= 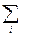 Xi,
Xi,
т.е. валовой продукт по формированию стоимости равен валовому продукту по направлениям его конечного использования;
2. 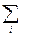 Yi =
Yi = 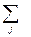 Zj,
Zj,
т.е. конечный продукт равен добавленной стоимости (факторным доходам);
3. 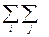 Xij =
Xij = 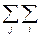 Xij,
Xij,
т.е. сумма текущих материальных затрат равна сумме возмещения промежуточного продукта.
Инструментом анализа макроэкономических показателей являются коэффициенты прямых и полных материальных затрат.
При этом предполагается, что объёмы производственного потребления прямо пропорциональны объёмам производства продукции потребляющих отраслей. Коэффициенты пропорциональности и являются коэффициентами прямых затрат аij, где аij = Xij/ Xj. Весь набор элементов аij составляет квадратную матрицу прямых затрат А, которая имеет размерность n´n.
Используя коэффициенты прямых затрат, формулу можно записать в следующем виде:
Xi = 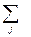 аij Xj + Yi , (при i = 1,2…,n).
аij Xj + Yi , (при i = 1,2…,n).
Тогда в векторно-матричной форме система уравнений распределения продукции выглядит так:
X=AX+Y,
где X – отраслевой вектор валового общественного продукта;
А – матрица коэффициентов прямых материальных затрат;
Y – отраслевой вектор конечного общественного продукта.
Решая это уравнение относительно вектора конечного общественного продукта Y, получим:
Y= (Е-А)Х.
Решая это уравнение относительно вектора валового выпуска по отраслям Х, получим:
Х=(Е-А)-1 Y,
где (Е-А)-1 – матрица коэффициентов полных материальных затрат, или матрица В. Леонтьева.
Элементы матрицы полных затрат отличаются от коэффициентов прямых затрат как количественно, так и качественно. Если коэффициенты прямых затрат аij характеризует усреднённый норматив расхода одной отрасли (поставщика) на единицу валовой продукции другой отрасли (потребителя), то коэффициенты полных материальных затрат bij характеризует все народнохозяйственные затраты (как прямые, так и косвенные) продукции данной отрасли (поставщика) на единицу конечной продукции другой отрасли (потребителя).
Дополнениями статической открытой модели МОБ являются:
во-первых, показатели характеризующие связь объёма производства с затратами первичных факторов производства, т.е. коэффициенты прямой трудоёмкости и фондоёмкости;
во-вторых, показатели, характеризующие функциональную структуру общественного продукта (конечного спроса), т.е. разбивку его на элементы: частное потребление, государственное потребление, инвестиции, чистый экспорт.
Модель межотраслевого баланса используется в прогнозировании в следующих целях:
· для прогнозирования объёмов отраслевого валового выпуска продукции, необходимых для обеспечения заданного объёма и структуры конечного спроса и матрице коэффициентов прямых затрат:
X= (E-A)-1Y
· для прогнозирования структуры и объемов конечного спроса при заданных объёмах отраслевого валового выпуска продукции и матрице коэффициентов прямых затрат:
Y=(E-A)X
· для прогнозирования отдельных элементов вектора валового продукта и конечного спроса по заданным заранее оставшимся элементам этих векторов:
X,Y=(E-A)(X,Y).
Рассмотрим пример прогнозирования валового отраслевого выпуска продукции при известном изменении объёмов конечного спроса на основе статической модели межотраслевого баланса. Предположим, что в прогнозируемом периоде не произойдёт изменение коэффициентов прямых и полных материальных затрат.
Пример. На основе данных межотраслевого баланса за отчетный период (таблица 3.6) составить прогноз валового выпуска продукции по отраслям, при условии, что в прогнозном периоде объём конечного спроса продукции по 1 отрасли увеличится на 5%, по 2 отрасли увеличится на 6% и по 3 отрасли увеличится на 7%.
Таблица 3.6 – Межотраслевой баланс за отчетный период
| 1-я отрасль | 2-я отрасль | 3-я отрасль | Yi | Xi | |
| 1-я отрасль | 32,4 | 13,6 | |||
| 2-я отрасль | |||||
| 3-я отрасль | 12,6 | 9,4 | |||
| Zj | |||||
| Xj |
Найдем коэффициенты прямых материальных затрат по формуле
аij = Xij/ Xj.

 А =
А = 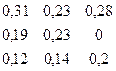
Из экономического смысла коэффициентов матрицы А следует, что величина а21=0,19 показывает, что на производство валовой продукции первой отрасли стоимостью 1 руб. потребуется продукции второй отрасли стоимостью 0,19 руб. Кроме продукции второй отрасли, для производства продукции первой отрасли понадобится продукция первой и третьей отраслей. Стоимость продукции этих отраслей в 1 рубле затрат на производство продукции первой отрасли составляет соответственно а11=0,31 и а31= 0,12. Таким образом, рассматривая столбец матрицы А, можно определить долю материальных затрат в стоимости определённого вида продукции. Так, для рассматриваемой продукции первой отрасли доля материальных затрат составляет 62% от объёма валовой продукции отрасли, следовательно, 38% затрат приходится на оплату труда, прибыль, амортизацию и т.д.
Матрицу коэффициентов полных материальных затрат определяют по формуле В =(Е-А)-1.

 В=
В= 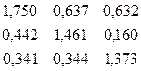
Определяем прогнозный объем конечного спроса:

 Yпрог =
Yпрог = 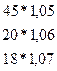
Согласно формуле X= (E-A)-1Y, определяем прогнозный объёма валового выпуска продукции по отраслям:
 |  |  |  |  |  |
X = 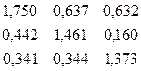 *
* 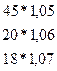 =
= 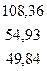
Ответ: При условии, что в прогнозном периоде произойдёт увеличение объёма конечного спроса по первой отрасли на 5%, тогда прогноз увеличения объёма валовой продукции составит 5,2% [(108,36/103)*100%]. При увеличении объёма конечного спроса по второй отрасли на 6% прогнозируется увеличение объёма валовой продукции на 5,6%, при увеличении объёма конечного спроса по третьей отрасли на 7% произойдёт увеличение валового выпуска продукции на 6%.
На основе МОБ, помимо определения объёмов валового выпуска отраслей и определения объёмов конечного спроса, в практике прогнозирования и анализа решается также задача определение равновесных цен.
Балансы затрат межотраслевого баланса производства и распределения продукции служат основой для изучения межотраслевых зависимостей цен. Рассматривая межотраслевой баланс по столбцам, можно исследовать ценовой аспект эффекта распространения в стране.
Столбец j межотраслевого баланса может быть представлен в следующем виде:
X1j +X2j + X3j +… + Xnj + Zj= Xj .
Если pi – цена единицы продукции в j отрасли; Xj¢ – объём выпуска продукции в натуральных единицах; аij¢ – коэффициент прямых материальных затрат в физическом выражении; rj – коэффициент добавленной стоимости j отрасли, тогда
pj Xj¢= 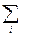 pi аij¢ Xj¢ + rj Xj¢ .
pi аij¢ Xj¢ + rj Xj¢ .
откуда
pj = 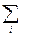 pi аij¢+ rj.
pi аij¢+ rj.
В матричном виде систему уравнений можно переписать как:
P= A¢ P + r, где A¢ – транспонированная матрица А, т.е. у неё взаимно переставлены столбцы и строки.
Решая уравнение относительно Р, получим
Р = (E – A¢)-1r = B¢r.
B¢ транспонированная матрица B.
Полученное уравнение называется межотраслевой моделью равновесных цен. Нетрудно установить взаимное соответствие этой модели и модели выпусков, а именно:
вектор объёма выпуска Х «вектор цен Р;
матрица коэффициентов полных материальных затрат В « ценовой матричный мультипликатор B¢;
вектор конечного спроса Y« вектор долей добавленной стоимости r.
Модель выпуска и ценовую модель называют двойственными.
На основе ценовой модели можно выяснить, как через посредничество структуры потребляемых каждой отраслью ресурсов измениться структура цен при варьировании величины добавленной стоимости.
Эффект распространения DР, вызванный изменением доли добавленной стоимости на D r, рассчитывается как
DР= B¢D r.
Если rj представить через сумму долей заработной платы rwj, прибыли rpj и остальной части добавленной стоимости rtj:
rj = rwj +rpj+rtj ,
то при росте заработной платы на a% изменение добавленной стоимости составит rwj +a rwj, а совокупное изменение цен
DР= ( rwj +a rwj )B¢.
Аналогичное изменение цен происходит при росте доли прибыли в общем объёме добавленной стоимости.
Рассматриваемая модель является полезным инструментом для прогнозирования вариантов экономической политики. С её помощью можно изучать влияние изменения цен и рентабельности в одних отраслях на уровни цен и доходов в других отраслях, влияние увеличения оплаты труда, изменение амортизационных отчислений, косвенных налогов на всю систему цен.
Рассмотрим пример: На основе данных межотраслевого баланса спрогнозировать эффект распространения для ценовых параметров при росте доходов занятых по найму в каждой отрасли на 10% (таблица 3.7).
Zj1 – доход занятых по найму;
Zj2 – предпринимательская прибыль
Zj3 –амортизационные отчисления, косвенные налоги и т.д.
Таблица 3.7 – Межотраслевой баланс
| 1-я отрасль | 2-я отрасль | 3-я отрасль | Yi | Xi | |
| 1-я отрасль | 32,4 | 10,6 | |||
| 2-я отрасль | |||||
| 3-я отрасль | 10,6 | 6,4 | |||
| Zj1 | |||||
| Zj2 | |||||
| Zj3 | |||||
| Zj | |||||
| Xj |



 Определяем коэффициенты прямых и полных материальных затрат:
Определяем коэффициенты прямых и полных материальных затрат:
А¢= 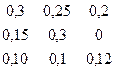 B¢=
B¢= 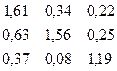
Находим эффект распространения для ценовых параметров при
росте доходов занятых по найму на 10%:
DР= B¢D r
За изменением доходов занятых по найму увеличивается доля добавленной стоимости в валовой продукции, её изменение определяется как rj+a rwj,, где rwj = Zj1/ Xj – доля заработной платы в валовом выпуске.
r1+a rw1= 49/108 + 0,1*24/108= 0,45+0,022=0,47;
r2+a rw2= 14/40 + 0,1*9/40=0,35 +0,023=0,372;
r3+a rw3= 36/53 +0,1*16/53 =0,68 +0,03 =0,71.




 Находим изменение ценовых параметров
Находим изменение ценовых параметров
 DР =
DР = 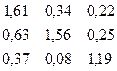 *
* 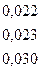 =
= 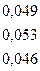
Определим, на сколько процентов изменилась добавленная стоимость в прогнозном периоде по формуле (a rwj/ rj)*100%:
(a rw1/ r1)*100%= (0,022/0,45)*100%=4,8%;
(a rw2/ r2)*100%= 6,6%; (a rw3/ r3)*100%=4,4%.
Определим, на сколько процентов изменилась цена в прогнозном периоде, по формуле (DРi/Рi)*100%:
(DР1/Р1)*100%= (0,049/1)*100%=4,9%;
(DР2/Р2)*100%=5,3% (DР3/Р3)*100%=4,6%.
Ответ запишем в виде таблицы:
| rj | Рi | rj+a rwj, | DРi + Рi | (a rwj/ rj)% | (DРi/Рi)% |
| 0,45 | 0,47 | 1,049 | +4,8 | +4,9 | |
| 0,35 | 0,37 | 1,053 | +6,6 | +5,3 | |
| 0,68 | 0,71 | 1,046 | +4,4 | +4,6 |
Ответ: При увеличении доходов занятых по найму на 10% по каждой отрасли, произойдет увеличение цены единицы продукции по первой отрасли на 4,9%, по второй отрасли – на 5,3%, по третьей отрасли – на 4,6%.
В дореформенный период в нашей стране велась серьёзная работа по межотраслевому балансу и балансу народного хозяйства, которая охватывала сферу материального производства. Ежегодно составлялись укрупнённые отчётные балансы по 18 отраслям, а с периодичностью в 10 лет разрабатывались межотраслевые балансы, охватывающие более 100 подотраслей. Проводились научные работы по натурально-стоимостным балансам размерностью около 500 продуктов. Из-за переходных процессов в экономике и обществе, серьёзных изменений первичной статистики в начале 90-х годов составление межотраслевых балансов было приостановлено. Однако в настоящее время происходит возрождение интереса к этому инструменту и работы по межотраслевым балансам возобновились.
Тестовые задания для самоконтроля:
1. Во втором квадранте межотраслевого баланса отражается:
101) факторные доходы;
102) отраслевая структура конечного спроса;
103) межотраслевые затраты;
104) трансформация факторных доходов в элементы конечного спроса.
2. Коэффициенты полных затрат межотраслевого балансового метода показывают:
201) сколько промежуточной продукции одной отрасли необходимо для производства валовой продукции другой отрасли;
202) сколько промежуточной продукции отрасли i необходимо для производства одной единицы валовой продукции отрасли j;
203) сколько валовой продукции отрасли i необходимо для производства одной единицы промежуточной продукции отрасли j;
204) сколько валовой продукции отрасли i необходимо для производства одной единицы конечной продукции отрасли j;
3. По какой формуле определяется объём добавленной стоимости в межотраслевом балансовом методе:
301) Xj = 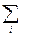 Xij+ Zj ;
Xij+ Zj ;
302) Zj = . Xj .- 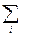 Xij ;
Xij ;
303) Zj = . Xi .- 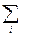 Xij ;
Xij ;
304) Xi = 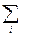 Xij+ Zj .
Xij+ Zj .
4. В состав элементов конечного спроса в межотраслевой балансовой модели входят элементы:
401) предпринимательская прибыль;
402) экспорт;
403) косвенные налоги;
404) инвестиции.
5. Модель межотраслевого баланса используется в прогнозировании для:
501) прогнозирования объёмов отраслевого валового выпуска продукции;
502) прогнозирования изменения цен на продукцию отраслей;
503) прогнозирования валютного курса;
504) прогнозирования объемов конечного спроса.
6. Какой метод даёт возможность получить оценки параметров тренда, характеризующих не средний уровень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения?
601) метод наименьших квадратов;
602) метод скользящей средней;
603) метод написания сценария;
604) метод экспоненциального сглаживания.
7. В прогнозировании экстраполяция (экстраполирование) применяется:
701) при изучении мнений экспертов;
702) при изучении временных рядов;
703) при изучении времени прогнозирования;
704) при анкетировании.
8. Продолжением уровней ряда динамики в прошлое – это
801) ретроспективная экстраполяция;
802) интерполяция;
803) перспективная экстраполяция;
804) простая экстраполяция.
9. Какой метод применяется в том случае, когда ряды динамики характеризуются резкими колебаниями показателей по годам:
901) метод наименьших квадратов;
902) метод скользящей средней;
903) метод написания сценария;
904) метод экспоненциального сглаживания.
10. Метод экспоненциального сглаживания позволяет:
1001) давать обоснованные прогнозы на основании рядов динамики, имеющих умеренную связь во времени, и обеспечивает большой учёт показателей, достигнутых в последние периоды наблюдения;
1002) отвлечься от случайных колебаний временного ряда путём замены значений внутри выбранного интервала средней арифметической величиной;
1003) минимизировать сумму квадратических отклонений между наблюдаемыми и расчётными величинами;
11. Задачами корреляционного анализа являются:
1101) установление числового значения параметров уравнения регрессии;
1102) определение вида уравнения регрессии;
1103) отбор факторов, оказывающих существенное влияние на результирующий признак;
1104) измерение степени связности двух и более явлений.
12. Коэффициент корреляции представляет собой:
1201) среднее квадратическое отклонение значений результирующего признака;
1202) эмпирическую меру линейной зависимости между фактором и результирующим показателем;
1203) сумму квадратов отклонений фактических значений от расчётных;
1204) случайную ошибку случайной бесповторной выборки.
13. Корреляционно-регрессионный анализ применяется в прогнозировании для:
1301) исследования интенсивности зависимости между явлениями;
1302) определения вида и формы зависимости между явлениями;
1303) исследования глубины зависимости между явлениями;
1304) определения важности зависимости между явлениями.
14. Зависимость между случайными величинами, при которой изменение одной величины влечёт за собой изменение закона распределения другой величины, называется:
1401) функциональной;
1402) условной;
1403) статистической;
1404) случайной.
15. Характеристика отклонения случайных величин от их средней величины – это:
1501) коэффициент доверия;
1502) величина генеральной совокупности;
1503) дисперсия значений признака в генеральной совокупности;
1504) предельная ошибка случайной бесповоротной выборки.
Дата добавления: 2020-03-17; просмотров: 1035;











