Информация в дискретных сообщениях.

Цель работы. Научиться практически определять количество информации в различного вида дискретных сообщениях.

Теоретическое обоснование. Количество информации, содержащееся в дискретном сообщении (I) можно найти из простого соотношения

I=n×H,

где n― число символов в сообщении,

H- энтропия источника сообщений, то есть среднее количество информации, приходящееся на один символ сообщения.

Энтропия источника сообщения определяется из основного соотношения теории информации (1.4), которое для удобства практического использования преобразуется к виду наиболее простому и удобному в зависимости от свойств дискретного источника сообщений.

В случае, если символы источника сообщения появляются равновероятно и взаимно независимо, то для подсчета энтропии такого рода сообщений используют формулу Хартли:

; ,

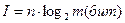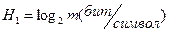где m- объем алфавита источника дискретных сообщений.

Если же символы источника сообщения генерируются с различными вероятностями, но взаимно независимы, то используют формулу Шеннона:

,

,

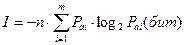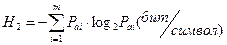где Р_аi ― вероятность появления символа a_i.

В случае же неравновероятного появления символов источника сообщения и наличия статистических зависимостей между соседними символами энтропию такого рода источника можно определить с помощью формулы Шеннона с условными вероятностями:

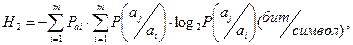
где 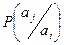― условная вероятность появления символа a_j после символа a_i.

Содержание работы.

1.Посчитать среднее количество информации, приходящееся на один символ источника дискретных сообщений (энтропию) в случаях:

а ―равновероятного и взаимно независимого появления символов;

б ―неравновероятного и взаимно независимого появления символов;

в ―при неравновероятном появлении символов и наличии статистических связей между соседними символами.

В качестве дискретного источника сообщений взять источник с объемом алфавита m = 34 (аналогичный по объему алфавита тексту на русском языке: 33 буквы и пробел), а его статистические характеристики смоделировать с помощью генератора случайных чисел.

2.Подсчитать количество информации в сообщении, представляющим собой Вашу фамилию, имя и отчество, считая, что символы сообщения появляются неравновероятно и независимо. Закон распределения символов найти путем анализа участка любого текста на русском языке длиной не менее 300 символов.

Выполнение работы. Работа выполняется на персональном компьютере в программном средстве «Mathcad». Так как в этом программном продукте в качестве встроенных функций используются только функции натуральных и десятичных логарифмов, то в процессе выполнения работы необходимо выполнить переход к логарифмам по основанию 2 по формуле перехода к иному основанию:

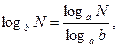
где а ― основание известных логарифмов;

б ― основание требуемых логарифмов;

N ― логарифмируемая величина.

П.1.а. Используя формулу Хартли, найти энтропию указанного источника дискретных сообщений (Н₁).

П.1.б. Смоделировать закон распределения символов дискретного источника сообщений, используя оператор rnd (A), который генерирует случайные числа из диапазона [0,A] по следующей программе:

m : =34 ― задание объема алфавита (m);

i : =1, 2,…,m ― i- порядковый номер символа алфавита;

r(i) :=rnd (1) ― генерирование 34 случайных чисел в интервале от 0 до 1;

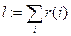― нахождение суммы всех r(i);

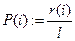― P(i) – вероятность появления i-го символа (a_i).

Проверить правильность вычислений, найдя сумму всех P(i) при i = 1,2,…,m.

Построить график закона распределения P(i) Используя формулу Шеннона, определить энтропию смоделированного источника дискретных сообщений (Н₂).

П.1.в.Смоделировать матрицу условных вероятностей появления символа a_j после символа a_i по следующей программе:

m : =34 -― задание объема алфавита (m);

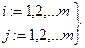― порядковый номер символа алфавита;

r(i,j) := rnd(1) ― генерирование матрицы (34×34) случайных чисел в интервале от 0 до1;

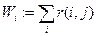― нахождение суммы элементов в каждой строке матрицы r(i,j);

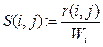―нормировка по строкам матрицы r(i,j) с целью получения суммы элементов в каждой строке, равной 1;

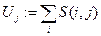― нахождение сумм элементов в каждом столбце матрицы S(i,j);

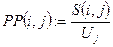― нормировка по столбцам матрицы S(i,j) с целью получения суммы элементов в каждом столбце равной 1.

Полученные значения элементов матрицы PP(i,j) приближенно можно считать условными вероятностями появления символа под номером j после i-го символа.

Используя формулу Шеннона с условными вероятностями определить энтропию смоделированного источника дискретных сообщений (Н₃).

П.2.Определить вероятность появления каждого символа (буквы) P_i путем деления числа появлений этого символа (a_i) на общее число символов (не менее 300), входящих в сообщение. В случае, если какой-либо символ (из m= 34) в сообщении не встретился, считать, что он встретился 1 раз, иначе может возникнуть неопределенность в формуле Шеннона. Отсутствие в исследуемом сообщении какого-либо символа из состава алфавита источника сообщений свидетельствует лишь о том, что анализируемое сообщение не содержит достаточного числа символов (не достаточно длинное), чтобы появились все символы входящие в алфавит.

Построить график закона распределения символов (букв)в сообщении.

Проверить правильность полученного закона распределения, для чего найти сумму вероятностей появления каждого символа. Эта сумма должна быть равна 1.

С помощью формулы Шеннона найти энтропию (Н₄) дискретного источника (текста на русском языке). Подсчитав число символов в Вашей фамилии, имени и отчестве (включая пробелы), найти количество информации, содержащейся в этом сообщении.

Разработать алгоритм и написать программу в программном средстве MathCad для автоматического нахождения вероятности появления каждого символа (буквы) P_i в избранном сообщении и определения энтропии (Н₅) дискретного источника (текста на русском языке)

Сравнить полученные результаты с результатами «ручного» нахождения вероятности появления каждого символа (буквы) P_i в избранном сообщении.

Пример программы, разработанной в программном средстве MathCad, для нахождения вероятности появления каждого символа (буквы) P_i в избранном сообщении представляется.

Контрольные вопросы.

1. Какие источники сообщений называют дискретными?

2. Для каких источников дискретных сообщений применимы формулы Хартли, Шеннона?

3. Каким образом описывается статистическая зависимость между соседними символами в дискретных сообщениях?

4. Дайте определение энтропии источника дискретных сообщений.

5. Как проверить правильность нахождения закона распределения символов источника дискретных сообщений?

6. Какой вид дискретных сообщений обладает наибольшей энтропией?