Информационная оценка датчиков сообщений

Согласно принятой общей информационной модели (Рис.4.1) первичное восприятие сообщений осуществляется датчиками сообщений. Датчик сообщений преобразует первичную естественную форму визуального сообщения в форму, удобную для последующей обработки, чаще всего в электрическую. Датчики принято характеризовать следующими основными параметрами:

1. Коэффициент преобразования 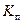, который определяется соотношением

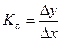, (4.33)

где 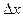- приращение первичного сообщения;

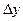- приращение выходной величины датчика.

Этот параметр характеризует лишь безынерционные и линейные датчики сообщений.

Датчик называют безынерционным, если 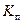не зависит от длительности приращения 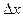, и линейным, если 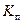не зависит от величины 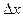. Линейность датчика характеризует степень приближения функции 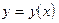к линейной зависимости.

Степень нелинейности датчика сообщений характеризуется коэффициентом нелинейных искажений.

2. Передаточная функция 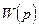- отношение преобразования Лапласа от выходной величины 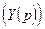к преобразованию Лапласа от первичного сообщения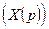

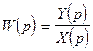, (4.34)

где

, .

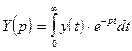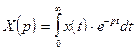3. Чувствительность - это минимальное значение сообщения, которое может быть преобразовано датчиком

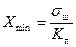, (4.35)

где 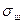- эффективная величина шумов датчика.

Зная основные технические параметры датчика можно найти основные информационные характеристики, присущие процессу преобразования исходного сообщения x в выходной сигнал датчика y, входящего в информационную модель (Рис.4.1).

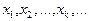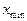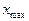Действительно, при неоднократном преобразовании символов исходного сообщения можно найти и - минимальное и максимальное значение входного сигнала датчика, соответствующего исходному сообщению. По этим значениям можно определить диапазон преобразуемого входного сигнала :

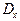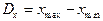. (4.36)

Из (4.35) следует, что для каждого датчика существует конкретное значение 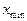(чувствительность датчика), определяемое уровнем шумов датчика. Чувствительность датчика 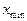определяет разрешающую способность датчика 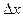, то есть ту минимальную разность между уровнями входного сигнала, при которой можно достоверно распознать отдельные символы исходного сообщения.

Так как диапазон входного сообщения ( 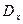) и разрешающая способность ( 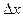) конечны, то возможно различить лишь конечное число уровней (N)

.

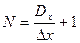Таким образом, объем алфавита входного сообщения не может быть больше N.

В случае отсутствия данных о законе распределения символов источника сообщения можно считать, что их появление равновероятно, и энтропия входного сообщения датчика H может быть найдена по формуле Хартли

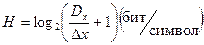. (4.37)

Если же появление символов неравновероятно, но известен закон распределения символов входного сообщения, то энтропия (H) определяется по формуле Шеннона

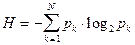, (4.38)

где 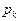- вероятность попадания в k уровень;

k - номер уровня.

При известной частоте измерений датчика - F (сек^-1) легко подсчитать входную производительность датчика

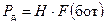. (4.39)

Для информационного согласования источника сообщений с датчиком сообщений необходимо, чтобы производительность источника сообщений 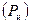не превышала входную производительность датчика сообщений 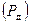, в противном случае неминуемы потери информации.

Воздействие шумов на датчик выражается не только в ограничении энтропии воспринимаемого сообщения, но и в потерях информации в процессе преобразования. Известно, что если на датчик воздействует некий аддитивный шум (n), то энтропия полезного сигнала 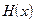, которую можно извлечь из смеси 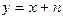, равна разности энтропий принятого сообщения 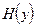и шума 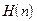, то есть

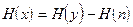. (4.40)

Заметим, что влияние шума (n) нарушает однозначную зависимость между входным сигналом x и выходным сигналом y и делает ее случайной (статистической).

В случае аддитивного шума закон распределения выходного сигнала y при фиксированном входном сигнале x равен закону распределения шума, то есть

,

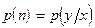где 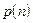- плотность распределения шума;

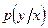- условная плотность распределения выходного сигнала y при известном входном сигнале x.

Тогда выражение (4.40) может быть записано в следующем виде:

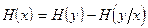. (4.41)

Подставив в это выражение соответствующие значения 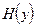и 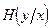, рассчитанные по формуле Шеннона, получим:

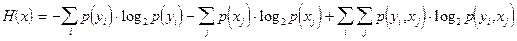, (4.42)

где 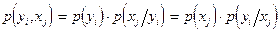- совместная плотность вероятности сигналов x и y;

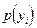- плотность вероятности выходного сигнала y;

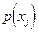- плотность вероятности входного сигнала x;

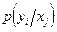и 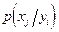- соответствующие условные плотности вероятности при фиксированном входном сигнале 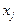и фиксированном выходном сигнале 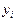соответственно.

Для случая непрерывных сигналов x и y выражение (4.42) после предельного перехода приобретет вид

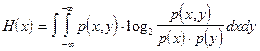, (4.43)

где 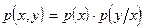- совместная плотность вероятности сигналов x и y;

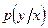- условная плотность вероятности сигнала y при фиксированном x;

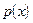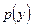, - плотность вероятности сигналов x и y соответственно.

Таким образом, датчик сообщения как элемент информационной системы требует согласования по информационным параметрам с источником сообщений с целью уменьшения (а в идеале устранения) потерь информации в процессе преобразования сообщений источника в иную форму, удобную для дальнейшего использования.

Для практического использования рассмотренные выше соотношения (4.40-4.43) не всегда удобны, так законы распределения символов входного сообщения (x) и шума (n) чаще всего неизвестны. Поэтому на практике целесообразно информационные свойства датчиков сообщений выражать через максимально возможную для данного датчика энтропию входного сообщения - 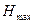, считая, что символы входного сообщения равновероятны и некоррелированы

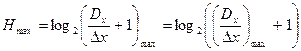, (4.44)

а входную производительность датчика характеризовать ее максимальным предельным значением :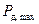

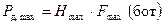, (4.45)

где 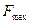- максимальная частота измерения датчика.

В сканирующих устройствах в качестве фотоэлектрического преобразователя (фотодатчика) используют полупроводниковые фотоприемники или фотоэлектронные умножители (ФЭУ), для которых основной причиной ограничения энтропии входного сообщения ( 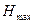) и входной производительности ( 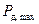) являются шумы фотометрирования, вызванные квантовой природой света и физической природой фотоприемников, причем энтропия входного сообщения ( 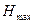) и частота измерения фотометрических параметров отдельных элементов изображения ( 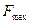) взаимозависимы.

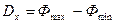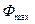Применительно к фотоприемникам диапазон преобразуемого входного сообщения , где и 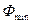- максимальное и минимальное возможные значения светового потока, падающего на фотоприемник, а в качестве разрешающей способности 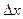целесообразно использовать среднеквадратическое эффективное значение шума фотоприемника, приведенное к его входу - 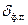. Тогда выражение (4.44) преобразуется к виду:

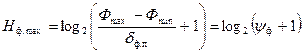, (4.46)

где 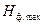- максимальная входная энтропия фотоприемника,

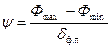- отношение сигнал/шум фотоприемника.

В фотоприемных устройствах основным видом шума является дробовой шум, представляющий собой флуктуации во времени электрического сигнала, вызванные тем, что электрический ток является потоком дискретных частиц, число которых подчиняется квантовым законам. Среднеквадратическое (эффективное) значение дробового шума ( 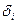) на выходе фотоприемника при заданном значении светового потока, падающего на фотоприемник (Ф) пропорционально полосе частот преобразуемых сигналов ( 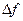) или обратно пропорционально времени измерения светового потока ( 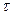). Известно выражение для нахождения среднеквадратического значения дробового шума на выходе фотоприемника (ФЭУ):

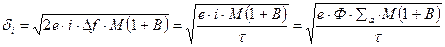, (4.47)

где 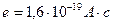- заряд электрона;

i - ток ФЭУ [А];

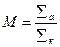- коэффициент усиления ФЭУ;

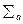- анодная чувствительность ФЭУ [А/Вт];

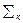- катодная чувствительность ФЭУ [А/Вт];

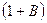- коэффициент, зависящий от конструкции ФЭУ, в среднем равный 2,5.

Аналогичные соотношения, связывающие среднеквадратическое значение дробового шума с техническими характеристиками фотоприемника и временем измерения характеристик элемента изображения известны и для полупроводниковых фотоприемников.

Приведя среднеквадратическое (эффективное) значение шума ко входу фотоприемника

,

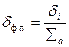и задаваясь отношением сигнал/шум на входе фотоприемника

,

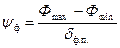с учетом (4.47) можно получить выражение для нахождения отношения сигнал/шум фотоприемника при заданной длительности измерения светового потока (τ):

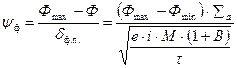. (4.48)

Следовательно, из (4.46) вытекает соотношение для определения максимальной входной энтропии фотоприемника:

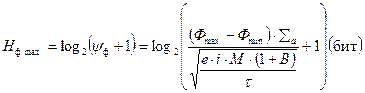. (4.49)

Исходя из общего вида информационной модели (Рис. 4.1), условием информационной согласованности источника сообщения и датчика сообщения, при выполнении которого обеспечивается преобразование исходного сообщения без потерь информации, будет:

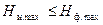, (4.50)

где 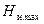- максимальное количество информации, которое может содержаться в символе источника сообщений (элементарной площадке).

Следовательно, должно выполняться условие:

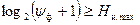. (4.51)

В случае использования в качестве источника сообщения оптических или фотоизображений их 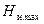может быть найдено на основе полученных соотношений (§4.2, §4.3), и из (4.51) легко определить требуемое отношение сигнал/шум фотоприемника ( ):

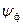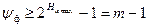, (4.51)

где m – объем алфавита источника сообщения,

а зная требуемое отношение сигнал/шум и значения технических параметров используемого фотоприемника из 4.48 легко получить соотношение для определения времени измерения характеристик элемента изображения (τ) при заданном отношении сигнал/шум:

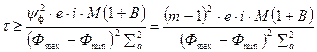. (4.52)

Таким образом, максимально возможное значение входной производительности фотоприемника ( 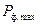) может быть найдено из следующих соотношений:

- при заданном τ

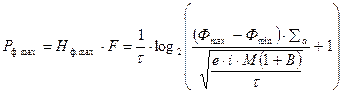; (4.53)

- при заданном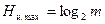

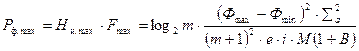; (4.54)

где 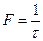, 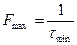- частота измерения датчика;

m - объем алфавита источника сообщения.