Эффективное кодирование неравновероятных символов источника дискретных сообщений.

<27 28 293031 32 33 >

Цель работы. Ознакомление с алгоритмами эффективного кодирования неравновероятных символов источника дискретных сообщений и сравнение их эффективности.

Содержание работы. По номеру в списке группы ( k ) из Таблицы 1 выбрать закон распределения вероятности появления символов источника дискретных сообщений с объёмом алфавита М=8.

Произвести эффективное кодирование заданного источника дискретных сообщений по алгоритму Шеннона-Фено и по алгоритму Хафмена.

Рассчитать для построенных на основе этих алгоритмов кодов:

а). среднюю длину неравномерного кода (n_н);

б). избыточность неравномерного кода(R_нк);

в). энтропию элементов символов полученных кодов(H_1н);

Сравнить полученные результаты с соответствующими параметрами равномерного двоичного цифрового кода.

Таблица 1.

m_i
m₁	0.10	0.18	0.07	0.65	0.55	0.60	0.01	0.15	0.30	0/01
m₂	0.51	0.10	0.03	0.05	0.05	0.06	0.02	0.10	0.20	0.05
m₃	0.02	0.47	0.11	0.06	0.16	0.02	0.02	0.30	0.10	0.03
m₄	0.10	0.07	0.33	0.03	0.03	0.10	0.15	0.35	0.05	0.02
m₅	0.02	0.03	0.25	0.02	0.02	0.02	0.02	0.02	0.15	0.10
m₆	0.20	0.02	0.01	0.15	0.02	0.15	0.45	0.02	0.10	0.14
m₇	0.01	0.04	0.17	0.02	0.02	0.03	0.30	0.01	0.07	0.25
m₈	0.04	0.09	0.03	0.02	0.15	0.05	0.03	0.05	0.03	0.40

2. Произвести эффективное кодирование двоичным кодом соответствующего Вашему номеру (k) источника дискретных сообщений по алгоритму Хаффмена в программном средстве MathCad. Вычислить энтропию сообщений и среднюю длину nсркодового слова. Сравнить с минимально возможной длиной nср.min.и средней длиной кодового символа при кодировании равномерным кодом. Сравнить полученный результат с результатами «ручного» кодирования.

Ниже приведён пример программы, разработанной в программном средстве MathCad, для эффективного кодирования двоичным кодом источника дискретных сообщений по алгоритму Хаффмена в программном средстве MathCad.

Источник дискретных сообщений X (xi, i= 1,…, m), c объёмом алфавита равном m = 9, имеет следующие вероятности их появлений, заданные при 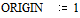вектор-строкой

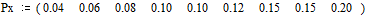где, например, 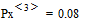и .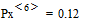

Предварительно определим единицы измерения количества энтропии и информации как 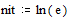и .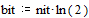

Составим матрицу, в которой вероятности выписываются в первый (основной) столбец в порядке их убывания, т.е.

;

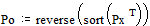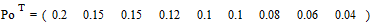Две последних вероятности P1 объединяются в одну вспомогательную вероятность Ps1:

.

; ; ;

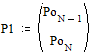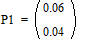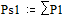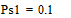
Вероятности

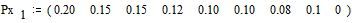
снова располагаются в порядке их убывания в дополнительном столбце

;

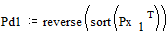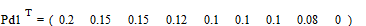Две последних вероятности P2 объединяются в одну вспомогательную вероятность Ps2:

.

; ; ;

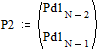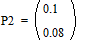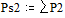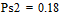
Вероятности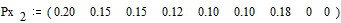

снова располагаются в порядке их убывания в дополнительном столбце

;

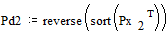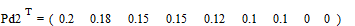Две последних вероятности P3 объединяются в одну вспомогательную вероятность Ps3:

.

; ; ;

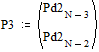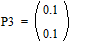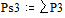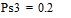
Вероятности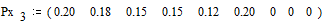

снова располагаются в порядке их убывания в дополнительном столбце

;

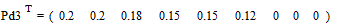Две последних вероятности P4 объединяются в одну вспомогательную вероятность Ps4:

.

; ; ;

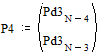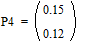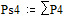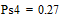
Вероятности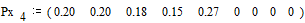

снова располагаются в порядке их убывания в дополнительном столбце

;

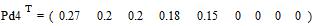Две последних вероятности P5 объединяются в одну вспомогательную вероятность Ps5:

.

; ; ;

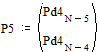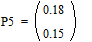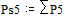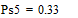
Вероятности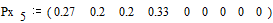

снова располагаются в порядке их убывания в дополнительном столбце

;

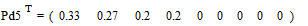Две последних вероятности P6 объединяются в одну вспомогательную вероятность Ps6:

.

; ; ;

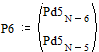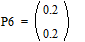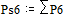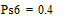
Вероятности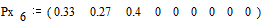

снова располагаются в порядке их убывания в дополнительном столбце

;

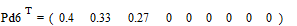Две последних вероятности P7 объединяются в одну вспомогательную вероятность Ps7:

.

; ; ;

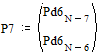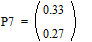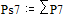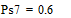
Вероятности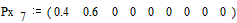

снова располагаются в порядке их убывания в дополнительном столбце

;

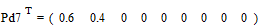Две последних вероятности P8 объединяются в одну вспомогательную вероятность Ps8:

.

; ; ;

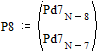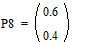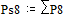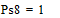
Вероятности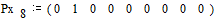

снова располагаются в порядке их убывания в дополнительном столбце

;

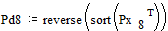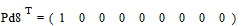На этом при получении дополнительного столбца с вероятностью, равной единице, процесс заканчивается. Матрица M, на основе которой проводится кодирование, принимает вид:

;

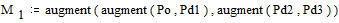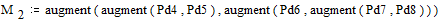На основании данной таблицы строим кодовое дерево, ветки которого соответствуют вероятностям, согласно матрице M.

Каждой ветке дерева присваивается символ "1" при выходе из узла вверх и символ "0" при выходе из узла вниз. Движение по кодовому дереву из вершины с P=1.00 к сообщениям, определяемым соответствующими вероятностями, дает двоичные кодовые комбинации эффективного кода, приведенные в таблице.

Сообщения	Вероятность	Двоичный код
x₁	0.04
x₂	0.06
x₃	0.08
x₄	0.10
x₅	0.10

x₆	0.12
x₇	0.15
x₈	0.15
x₉	0.20

Согласно таблице кодирования, длину кодовых символов можно описать вектор-строкой

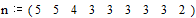Средняя длина кодового слова в битах

; .

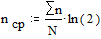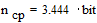Энтропия источника сообщений

; .

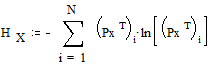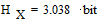На основании (4.2) минимально возможная средняя длина кодового слова равна энтропии источника, т.е.

; .

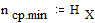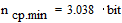В случае использования равномерного двоичного кодирования девяти символов сообщения требуется четырехразрядное кодовое слово для каждого сообщения, так как 23<9. При таком кодировании максимальная средняя длина кодового слова bit.

Таким образом, проведенное кодирование более эффективно, чем равномерное. Однако оно не достигает максимально возможной эффективности, так как ncp.min< ncp< ncp.max.

Контрольные вопросы.

Какой вид кодирования называют эффективным и в чем его специфика?
Что такое избыточность кодов?
Какие коды называются равномерными?
На каких принципах основано построение эффективных кодов при неравновероятном появлении символов сообщения?
Принцип построения эффективного кода по алгоритму Шеннона-Фено.
Принцип построения эффективного кода по алгоритму Хафмена.