Классическое вариационное исчисление

До сих пор мы рассматривали задачи, где решением являлся некоторый вектор 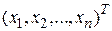. Однако существуют задачи оптимизации, где решение не является вектором, а представляет собой функцию 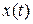вещественного переменного 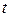на некотором интервале 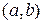, так называемую экстремаль. Так как график вещественной функции представляет собой бесконечное множество значений, можно говорить, что речь идет о задаче оптимизации бесконечной размерности.

Для того, чтобы можно было сравнивать различные функции-решения между собой, каждой функции ставится в соответствие число, или, как обычно говорят, задается функционал, экстремум которого необходимо найти.

Все методы поиска экстремумов функционалов можно разделить на три группы: классическое вариационное исчисление (использование уравнения Эйлера), принцип максимума и динамическое программирование.

Классическое вариационное исчисление является исторически наиболее ранним и разработано для задач, где экстремалями являются гладкие функции. Рассмотрим типовую постановку задачи вариационного исчисления на примере нескольких простых задач, начав с задачи о брахистохроне, с которой собственно и началось данное направление математики.