Типовые задачи вариационного исчисления.

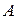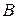Задача о брахистохроне.Задача была поставлена Иоганном Бернулли в июне 1696 года. Он предложил ведущим математикам мира решить следующую задачу: даны две точки и , лежащие в вертикальной плоскости. Какова траектория точки, движущейся только под действием силы тяжести, которая начинает двигаться из 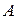и достигает точки 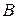за кратчайшее время?

На предложение И.Бернулли откликнулись такие математики как И.Ньютон, Я.Бернулли, Г.Лейбниц, Г.Лопиталь. Все они разными методами решили эту задачу. Из различных методов наиболее перспективным оказался метод И.Ньютона, который и стал основой важнейшего направления математики – вариационного исчисления.

В данный момент нас интересует постановка задачи.

Введем систему координат, поместив начало координат в точку 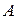и направив ось 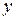вниз. Тогда в начальный момент времени 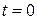материальная точка имеет координаты (0,0). Пусть в конечный момент времени тело должна оказаться в точке 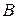с координатами 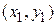. Кривую спуска будем искать в виде функциональной зависимости 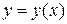. В силу выбора направления осе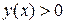й при .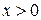

Всякой кривой 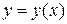, соединяющей точк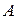и и 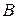, поставим в соответствие время скатывания 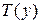. Величина 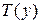является функционалом, поскольку аргументом 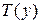является функция 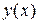. При 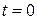должно быть 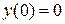, при ­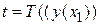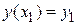- . Таким образом, поставлена задача о минимизации функционала при условии закрепления концов.

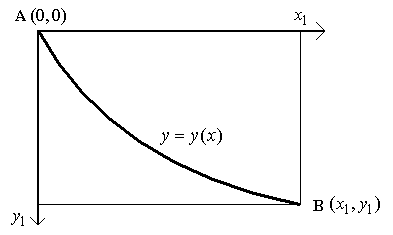
Рис. 5.1. Задача о брахистохроне

Получим выражение для 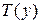. Скорость скатывания можно записать как 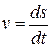, где 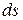- дифференциал дуги кривой. Тогда 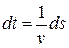. Отсюда можно найти время спуска как интеграл 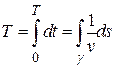, где 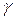– график кривой .

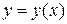Задача свелась к вычислению криволинейного интеграла 1-го типа. Так как кривая задана в явном виде, дифференциал кривой можно записать как 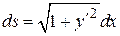. Тогда

.

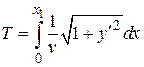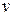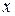Осталось выразить через и .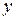

Пусть частица массой 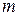находится на высоте 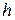, а ее скорость равна 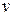. Тогда ее потенциальная энергия равна 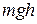, а кинетическая – 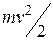. Если частица движется только под действием силы тяжести, то сумма потенциальной и кинетической энергии постоянна. Отсюда скорость частицы 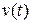и высота 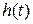связаны соотношением .

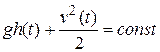Пусть начальная скорость частицы нулевая. Тогда, согласно закону Галилея, частица на высоте 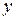будет двигаться со скоростью 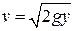. Таким образом, время скатывания 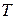материальной точки по кривой 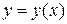равняется 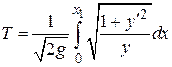, т.е является функционалом от траектории.

Задача о наибольшей площади (Задача Дидоны). Зада́ча Дидо́ны связана с древней легендой об основании города Карфагена. Дидона – сестра царя финикийского города Тира, переселилась на южное побережье Средиземного моря, где попросила у местного племени участок земли, который можно охватить шкурой быка. Местные жители предоставили шкуру, которую Дидона разрезала на узкие ремни и связала их. Получившимся канатом охватила территорию у побережья. Возникает вопрос о том, как можно захватить максимальную площадь при ограничениях на длину каната.

Сформулируем эту задачу так: среди всех плоских кривых, имеющих данную длину 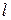и оканчивающихся в точках А(а,0) и 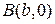, найти кривую, ограничивающую вместе с отрезком 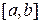оси 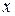область с наибольшей площадью.

Пусть уравнение кривой будет 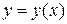. Задача заключается в том, чтобы найти функцию 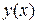, удовлетворяющую краевым условиям 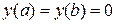и тождеству 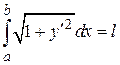и сообщающую интегралу 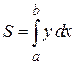наибольшее значение.

Общим для рассмотренных задач является то, что каждый раз ищется функция, удовлетворяющая тем или иным поставленным условиям и сообщающая экстремальное значение заданному функционалу.