Необходимые условия экстремума. Уравнение Эйлера.
Сформулируем задачу. Пусть задан функционал вида
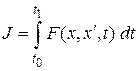 .
.
Требуется найти функцию 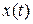 , которая дает ему минимум. Геометрически это можно трактовать так. Даны две точки
, которая дает ему минимум. Геометрически это можно трактовать так. Даны две точки 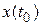 и
и 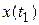 . Нужно найти уравнение линии, проходящей через эти две точки, которое при подстановке в функционал давало бы ему экстремум. Предположим, что такая функция
. Нужно найти уравнение линии, проходящей через эти две точки, которое при подстановке в функционал давало бы ему экстремум. Предположим, что такая функция 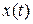 найдена (рис.5.2).
найдена (рис.5.2).
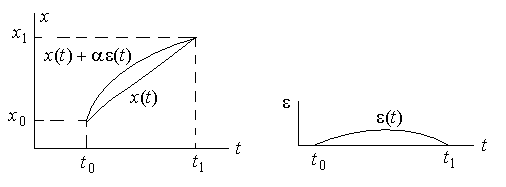
Рис. 5.2. Вариация функционала
Проварьируем ее и найдем приращение функционала
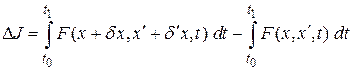 .
.
Вариацию 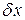 выбираем так, что
выбираем так, что 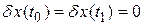 , т. е. любая линия проходит через заданные точки. Запишем выражение для первой вариации функционала
, т. е. любая линия проходит через заданные точки. Запишем выражение для первой вариации функционала
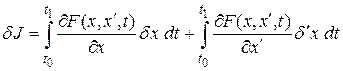 .
.
Интегрируем второе слагаемое по частям, пользуясь известной формулой 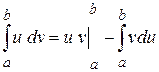 .
.
Получим
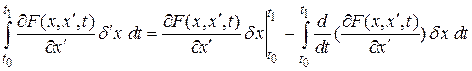 .
.
Первый член равен нулю, т.к. 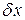 равно нулю при
равно нулю при 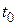 и
и 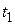 . Тогда общее выражение запишется
. Тогда общее выражение запишется
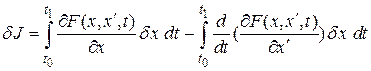 ,
,
или
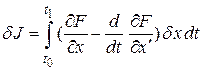 .
.
По теореме об экстремуме функционала, если 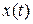 есть решение задачи, то
есть решение задачи, то 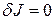 . Учитывая, что функция
. Учитывая, что функция 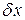 произвольна, можно записать необходимое условие экстремума в виде
произвольна, можно записать необходимое условие экстремума в виде
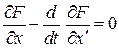 , или, как часто пишут
, или, как часто пишут
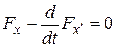 ,
,
где 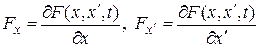 .
.
Полученное уравнение называется уравнением Эйлера и представляет собой необходимое условие, которому должны удовлетворять функции, обеспечивающие экстремум функционала 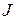 . Уравнение Эйлера является дифференциальным, в общем случае нелинейным уравнением второго порядка. Его решения
. Уравнение Эйлера является дифференциальным, в общем случае нелинейным уравнением второго порядка. Его решения 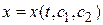 , где
, где 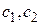 – постоянные интегрирования, являются экстремалями.
– постоянные интегрирования, являются экстремалями.
Поскольку уравнение Эйлера определяет только необходимое условие экстремума, нельзя утверждать, что решение уравнения Эйлера обеспечивает экстремум функционала. Это аналогично случаю, имеющему место при исследовании экстремумов функций: точка, где дифференциал функции равен нулю, может являться точкой перегиба, а не экстремума. Однако только среди решений Эйлера (экстремалей) следует искать функцию, которая доставляет экстремум функционалу. При этом постоянные 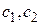 определяются из граничных условий.
определяются из граничных условий.
Условия Лежандра. Чтобы оценить, действительно ли решения уравнения Эйлера обеспечивают экстремум, а еще точнее максимум или минимум, необходимо провести дополнительные исследования. О характере экстремума можно судить по знаку второй вариации функционала 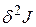 . Известно, что знак второй вариации совпадает со знаком производной
. Известно, что знак второй вариации совпадает со знаком производной
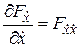 .
.
В связи с этим для достижения функционалом 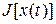 минимума на функции
минимума на функции 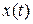 необходимо, чтобы выполнялось условие
необходимо, чтобы выполнялось условие
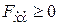 , (5.1)
, (5.1)
а для достижения максимума – условие
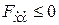 . (5.2)
. (5.2)
Условия (5.1), (5.2) называются условиями Лежандра и относятся к числу необходимых.
Таким образом, если некоторая функция реализует экстремум функционала, то она должна удовлетворять уравнению Эйлера и условию Лежандра в силу их необходимости. Обратное утверждение в общем случае не справедливо. Могут существовать функции, которые удовлетворяют уравнению Эйлера и условию Лежандра, но не доставляют экстремум функционалу. Исключить из рассмотрения подобные случаи можно при помощи достаточных условий экстремума. Но при решении практических задач наличие экстремума и его характер, как правило, заранее известны из экспериментальных исследований или предварительных расчетов. Это обстоятельство существенно упрощает решение вариационной задачи, давая возможность определить искомую функцию с помощью только необходимых условий и, в частности, с помощью только уравнений Эйлера.
Пример.Определим функцию 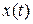 , обеспечивающую экстремум функционалу
, обеспечивающую экстремум функционалу
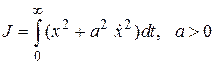 .
.
Функция 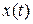 должна удовлетворять граничным условиям:
должна удовлетворять граничным условиям: 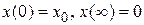 .
.
Находим частные производные 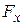 и
и 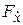 :
:
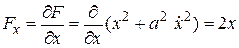 ;
;
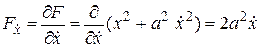 .
.
Отсюда уравнение Эйлера можно записать
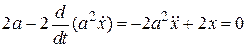 или
или 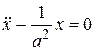 .
.
Решение этого уравнения имеет вид
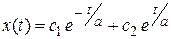 .
.
Граничные условия выполняются при 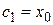 и
и 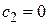 , поэтому окончательное решение имеет вид
, поэтому окончательное решение имеет вид
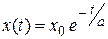 .
.
Дата добавления: 2020-03-17; просмотров: 1066;











