Симплекс-метод решения задачи линейного программирования.
Суть симплекс-метода состоит в следующем. Прежде всего, находим какое-то допустимое базисное решение, приняв 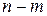 произвольных переменных равными нулю и решив получившуюся систему уравнений. Если при этом некоторые переменные получатся меньше нуля, следует выбрать иной базис. (Если во всех случаях получаются переменные меньшие нуля, то задача неразрешима, т.к. ограничения несовместны).
произвольных переменных равными нулю и решив получившуюся систему уравнений. Если при этом некоторые переменные получатся меньше нуля, следует выбрать иной базис. (Если во всех случаях получаются переменные меньшие нуля, то задача неразрешима, т.к. ограничения несовместны).
После этого проверяем, не достигнут ли уже максимум целевой функции  . Если нет, то ищем другое допустимое базисное решение, но не любое, а то, что ведет к увеличению
. Если нет, то ищем другое допустимое базисное решение, но не любое, а то, что ведет к увеличению  . Затем процедуру повторяем.
. Затем процедуру повторяем.
Разберем метод на нашем примере.
Как и ранее выберем в качестве свободных переменных 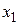 и
и 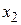 . Примем для них нулевые значения и подставим в (4.4). Получим систему трех уравнений для трех неизвестных. Решим полученную систему уравнений. Получили
. Примем для них нулевые значения и подставим в (4.4). Получим систему трех уравнений для трех неизвестных. Решим полученную систему уравнений. Получили 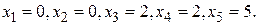 При этом
При этом 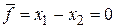 .
.
В целевую функцию переменная 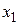 входит со знаком +. Если ее сделать базисной, то она увеличится и вся целевая функция станет больше. При этом переменная
входит со знаком +. Если ее сделать базисной, то она увеличится и вся целевая функция станет больше. При этом переменная 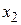 останется прежней.
останется прежней.
Таким образом, признаком того, что целевая функция не достигла максимума является то, что какая-то свободная переменная входит в 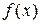 с плюсом.
с плюсом.
Но если 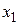 станет базисной, то какая-то другая переменная должна стать свободной. Вопрос – какая именно?
станет базисной, то какая-то другая переменная должна стать свободной. Вопрос – какая именно?
Для определения новой свободной переменной выразим базисные переменные через свободные. Получим
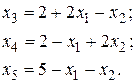
Из уравнений видно, что при 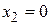 увеличение
увеличение 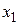 не уменьшает
не уменьшает 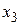 , но уменьшает
, но уменьшает 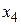 и
и 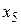 . В качестве новой свободной переменной принимается та переменная, которая первой превращается в нуль при увеличении
. В качестве новой свободной переменной принимается та переменная, которая первой превращается в нуль при увеличении 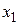 . Такой переменной является переменная
. Такой переменной является переменная 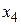 . Она достигает нуля при
. Она достигает нуля при 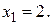 Таким образом, переменную
Таким образом, переменную 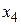 следует сделать свободной, что приводит к новому базису
следует сделать свободной, что приводит к новому базису 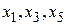 .
.
Для продолжения решения разрешим исходную систему (4.4) относительно новых переменных, приведя ее к виду
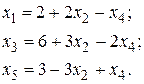
Целевую функцию также выразим через новые свободные переменные
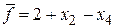 .
.
Повторяя прежние рассуждения, делаем вывод, что максимум 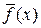 не достигнут, так как, увеличивая
не достигнут, так как, увеличивая 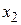 , можно увеличить целевую функцию. Для этого нужно перевести
, можно увеличить целевую функцию. Для этого нужно перевести 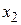 в базисные переменные, а базисную переменную
в базисные переменные, а базисную переменную 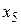 - в свободные.
- в свободные.
Разрешаем (4.4) относительно базиса 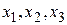 . Операция разрешения может представлять серьезные трудности. Универсальнее всего, воспользоваться матричными преобразованиями. Для этого перепишем (4.4) в виде
. Операция разрешения может представлять серьезные трудности. Универсальнее всего, воспользоваться матричными преобразованиями. Для этого перепишем (4.4) в виде
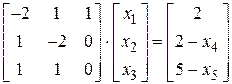 .
.
Тогда решение можно получить через выражение
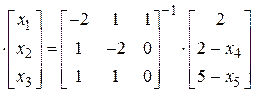 .
.
В данном случае получим
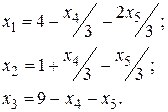
Целевая функция при этом принимает вид 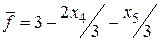 .
.
Из полученного выражения для целевой функции видно, что увеличение свободных переменных может привести только к уменьшению  . Это означает, что максимум достигнут. Он равен 3. Решением являются следующие значения переменных
. Это означает, что максимум достигнут. Он равен 3. Решением являются следующие значения переменных
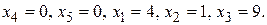
Недостаток рассмотренного метода в том, что он связан с громоздкими преобразованиями системы линейных уравнений из одной формы в другую. Значительного упрощения можно добиться, если формализовать метод путем представления уравнений в виде таблиц. Этот путь детально рассмотрен в методических указаниях по ИДЗ.
Дата добавления: 2020-03-17; просмотров: 767;











