Вариация функционала

Вариация функционала играет в вариационном исчислении ту же роль, что понятие дифференциала при изучении функций. Для ее вычисления при конкретных расчетах применяется формула Тейлора разложения в степенной ряд.

Пусть задан функционал 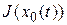. Придав функции 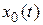малое приращение 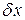, перейдем к некоторой другой близкой функции 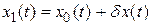. Новое значение функционала можно записать

.

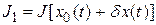Разложим функционал 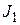в ряд по формуле Тейлора в окрестности точки .

.

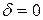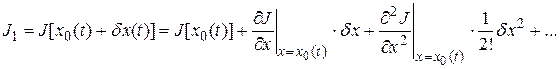Тогда приращение функционала запишется

.

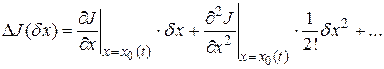Первый член ряда

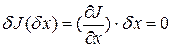представляет собой главную линейную часть приращения функционала и называется первой вариацией функционала.

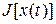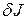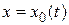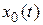Теорема. Если функционал , имеющий вариацию , достигает максимума или минимума при , где – внутренняя точка области определения функционала, то при 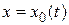вариация .

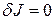Примем это утверждение без доказательства.

Условие 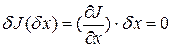при любых значения 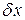(а на характер 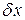не накладывается ограничений), может выполняться только при .

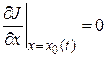Вторая вариация функционала представляет собой второй член ряда 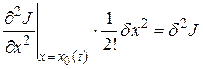. Она позволяет определить характер экстремума. Если 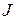достигает минимума, то 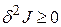, если максимума – .

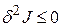Таким образом, мы определили в общем виде необходимые условия экстремума любого функционала. Они сводятся к равенству нулю первой вариации этого функционала. Перейдем теперь к более детальному анализу этой проблемы для конкретных видов функционалов.