Общие сведения о линейном программировании

Линейное программирование – направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности.

К математическим задачам линейного программирования обычно относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.

Круг задач, решаемых при помощи методов линейного программирования достаточно широк. Это, например:

· задача об оптимальном использовании ресурсов при производственном планировании;

· задача о смесях (планирование состава продукции);

· задачи о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или "задача о рюкзаке");

· транспортные задачи (анализ размещения предприятия, перемещение грузов) и т.д.

Линейное программирование – наиболее разработанный и широко применяемый раздел математического программирования (кроме того, сюда относят: целочисленное, динамическое, нелинейное, параметрическое программирование). Это объясняется следующим:

· математические модели большого числа экономических задач линейны относительно искомых переменных;

· данный тип задач в настоящее время наиболее изучен. Для него разработаны специальные методы, с помощью которых эти задачи решаются, и соответствующие программы для ЭВМ;

· некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.

Как уже отмечалось, математическая модель любой задачи математического программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы уравнений или неравенств; требование неотрицательности переменных.

Наиболее простым и часто встречающимся является случай, когда целевая функция и уравнения для ограничений линейны и каждое из выражений имеет вид:

.

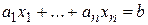В этом случае имеет место задача линейного программирования. Подсчитано, что в настоящее время примерно 80-85% всех решаемых на практике задач оптимизации относятся к задачам линейного программирования.

Первые исследования в области линейного программирования, ставившие своей целью выбор оптимального плана работы в рамках производственного комплекса, относятся к концу 30-х годов нашего века и связаны с именем Л.В. Канторовича. В отечественной научной традиции именно его принято считать первым разработчиком этого метода.

В 1938 г. он был на­значен консультантом в лабораторию фанерной фабрики и перед ним была по­ставлена задача разработать такой ме­тод распределения ресурсов, который мог бы максимизировать производительность оборудования. Канторович, сформули­ровав проблему с помощью математиче­ских терминов, произвел максимизацию линейной функции, подверженной боль­шому количеству ограничителей. Не имея чистого экономического образо­вания, он, тем не менее, понял, что максими­зация при многочисленных ограниче­ниях – это одна из основных экономиче­ских проблем и что метод, облегчающий планирование на фанерных фабриках, может быть использован во многих дру­гих производствах.

Говоря о развитии этого метода на Западе, следует сказать об американском экономисте-математике Тьяллинге Купмансе. Купманс пытался так разработать маршруты морских перевозок, чтобы снизить до минимума затра­ты на доставку грузов. Эта работа предоста­вила возможность Купмансу применить свои математические знания к решению фун­даментальной экономической проблемы – оптимальному распределению дефицитных ресурсов между конкурирующими потребителями.

В 1975 году Л.В. Канторовичу и Тьяллингу Ч. Купмансу была присуждена Нобелевская премия «за вклад в теорию оптимального распределения ресурсов».