Постановка задачи линейного программирования

Дана система 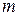линейно независимых уравнений с неизвестными 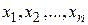, называемая системой ограничений задачи линейного программирования:

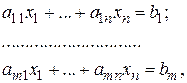(4.4)

где, не уменьшая общности, можно считать 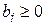. Характерной чертой данной задачи является то, что число уравнений меньше числа неизвестных, т.е. . Требуется найти неотрицательные значения переменных 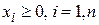, которые удовлетворяют уравнениям (5.1) и доставляют минимум целевой функции

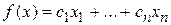, (4.5)

называемой линейной формой.

Более компактно задача может быть записана в матричной форме как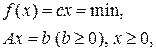

где 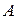- матрица размера ;

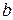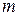- -мерный вектор;

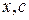- -мерные векторы.

Известно, что если в системе (4.4) число уравнений равно числу неизвестных, т.е. 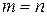, и определитель системы не равен нулю, то система имеет единственное решение. Если же число уравнений меньше числа неизвестных, то система уравнений имеет бесчисленное число решений. Условимся каждый набор переменных 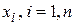удовлетворяющий системе уравнений (4.4), называть решением.

При этом на переменные 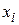наложено дополнительное ограничение 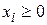. В общем случае таких решений также может быть много. Будем называть их допустимыми решениями. Таким образом, суть задачи линейного программирования состоит в том, чтобы из множества допустимых решений выбрать одно, которое дает минимум линейной форме (4.5).

Иногда в задаче линейного программирования все или некоторые уравнения (4.4) имеют вид неравенств вида

,

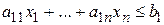или

.

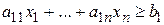Такие неравенства легко превратить в равенства введя добавочную переменную 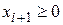так, чтобы имело место равенство. Размерность задачи при этом повышается, но она сводится к стандартному виду.

Поскольку в уравнениях (4.4) , некоторое произвольное решение можно найти, если приравнять нулю 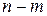переменных. Если при этом определитель полученной системы 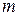-ого порядка будет отличен от нуля, то решение будет единственным. В линейном программировании такое решение называется базисным.

Базисом в линейном программировании называют любой набор из 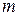переменных, таких, чтобы определитель полученной системы был отличен от нуля. Эти 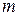переменных называют базисными, остальные 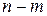– свободными. Обычно могут существовать несколько базисов с различными базисными переменными.

Если положить свободные переменные равными нулю и решить полученную систему уравнений, то получим базисное решение. Если при этом некоторые переменные в базисном решении получаются отрицательными, то такое базисное решение называется недопустимым.