Условная оптимизация. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Классическая задача минимизации состоит в нахождении минимума целевой функции 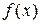 , где
, где 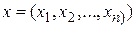 - точка в пространстве
- точка в пространстве 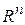 при наличии ограничений типа равенств
при наличии ограничений типа равенств
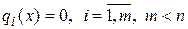 . (4.1)
. (4.1)
Если ограничения имеют место, то минимум функции называется условным минимумом. Если ограничения отсутствуют, то говорят о безусловном минимуме, нахождение которого сводится к определению и исследованию стационарных точек функции 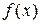 .
.
Основная проблема условной минимизации в том, что здесь уже нельзя пользоваться аппаратом стационарных точек, приравнивая к нулю производные по переменным, т.к. минимум, в общем случае, достигается в других точках. Очевидный путь решения задачи состоит в том, чтобы каким либо образом попытаться свести задачу условной минимизации к задаче безусловной минимизации.
Классический способ решения данной задачи состоит в том, что уравнения (4.1) используются для исключения из рассмотрения 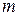 переменных. При этом целевая функция сводится к виду
переменных. При этом целевая функция сводится к виду
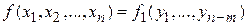 ,
,
где через 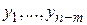 обозначены не исключенные переменные. Теперь задача состоит в нахождении значений
обозначены не исключенные переменные. Теперь задача состоит в нахождении значений 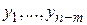 , которые обращают в минимум функцию
, которые обращают в минимум функцию 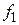 и на которые не наложено никаких ограничений, т.е. сводится к задаче на безусловный экстремум.
и на которые не наложено никаких ограничений, т.е. сводится к задаче на безусловный экстремум.
Пример.Пусть 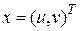 и требуется найти минимум целевой функции
и требуется найти минимум целевой функции
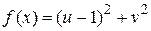
при ограничении 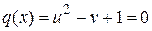 .
.
На рис. 4.1. изображены ограничения 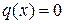 и линии уровня
и линии уровня 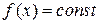 . Целевая функция описывает окружность с центром в точке (1,0). Ограничение – параболу, симметричную относительно оси
. Целевая функция описывает окружность с центром в точке (1,0). Ограничение – параболу, симметричную относительно оси 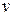 .
.
Оптимальное решение 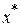 получается в точке касания кривых
получается в точке касания кривых 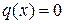 и
и 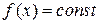 .
.
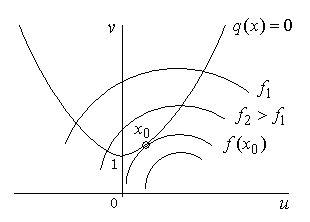
Рис. 4.1. Графическое решение задачи условной оптимизации
Для получения аналитического решения из уравнения 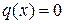 находим
находим 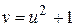 . Подставив полученное выражение в
. Подставив полученное выражение в  , получим
, получим
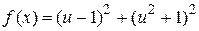 .
.
Дифференцируя это выражение по 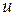 , приходим к уравнению
, приходим к уравнению 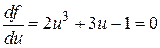 , которое имеет единственный вещественный корень
, которое имеет единственный вещественный корень 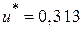 . При этом
. При этом 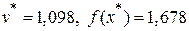 .
.
Легко определить, что при отсутствии ограничения 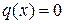 минимум достигается в точке
минимум достигается в точке 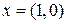 и равен нулю. Таким образом, ограничение приводит к увеличению значения целевой функции, т.е. к ухудшению качества оптимума.
и равен нулю. Таким образом, ограничение приводит к увеличению значения целевой функции, т.е. к ухудшению качества оптимума.
Если ограничения имеют сложный вид, то исключить с их помощью 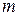 переменных из функции
переменных из функции 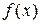 представляет серьезную проблему. Для аналитического решения такой задачи может использоваться метод сведения задачи на условный экстремум к задаче на безусловный экстремум, основанный на использовании множителей Лагранжа.
представляет серьезную проблему. Для аналитического решения такой задачи может использоваться метод сведения задачи на условный экстремум к задаче на безусловный экстремум, основанный на использовании множителей Лагранжа.
Метод множителей Лагранжа.Введем в рассмотрение вектор 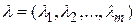 и исследуем свойства функции
и исследуем свойства функции
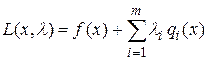
Функцию 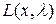 называют функцией Лагранжа а величины
называют функцией Лагранжа а величины 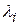 - множителями Лагранжа. Как видно, эта функция зависит от
- множителями Лагранжа. Как видно, эта функция зависит от 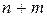 переменных
переменных 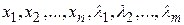 . Рассмотрим стационарные точки функции
. Рассмотрим стационарные точки функции 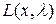 , которые получим, приравняв нулю частные производные по
, которые получим, приравняв нулю частные производные по 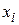 и
и 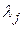 :
:
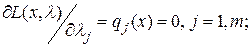 (4.2)
(4.2)
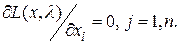 (4.3)
(4.3)
Видно, что уравнения (4.2) совпадают с ограничениями (4.1) и при их выполнении имеет место 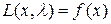 . Поэтому, если в стационарной точке
. Поэтому, если в стационарной точке 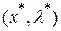 функция
функция 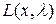 достигает минимума, то
достигает минимума, то 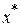 обеспечивает минимум функции
обеспечивает минимум функции 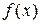 , т.е. дает решение задачи. Таким образом, задача на условный экстремум функции
, т.е. дает решение задачи. Таким образом, задача на условный экстремум функции 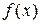 при наличии ограничений типа равенств, сводится к задаче определения стационарных точек функции Лагранжа, т.е. к задаче на безусловный экстремум.
при наличии ограничений типа равенств, сводится к задаче определения стационарных точек функции Лагранжа, т.е. к задаче на безусловный экстремум.
Рассмотрим применение технологии множителей Лагранжа к предыдущей задаче. Функция Лагранжа для этой задачи имеет вид
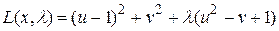 .
.
Дифференцируя данную функцию по 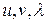 , получим три уравнения
, получим три уравнения
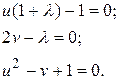
Выразим из первого уравнения 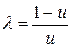 и подставим во второе. Имеем
и подставим во второе. Имеем 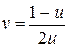 . Подставив полученный результат в третье уравнение, получим
. Подставив полученный результат в третье уравнение, получим 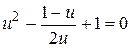 или
или 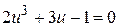 , что совпадает с уравнением для экстремума по переменной
, что совпадает с уравнением для экстремума по переменной 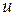 , полученным ранее методом подстановки. Соответственно и значения
, полученным ранее методом подстановки. Соответственно и значения 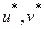 будут теми же самыми.
будут теми же самыми.
Дата добавления: 2020-03-17; просмотров: 770;











