Ограничения на допустимое множество

Наиболее типичный способ определения допустимого множества 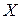- введение ограничений на переменные типа

, ,

, ,

, ,

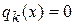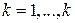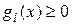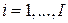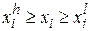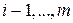а также требования неотрицательности всех или некоторых переменных. Если ограничений несколько, то допустимое множество решений задачи оптимизации является пересечением всех множеств, определяемых ограничениями.

Рассмотрим пример. Пусть для двумерной переменной 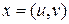заданы два ограничения:

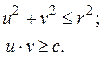
Первое ограничение определяет круг радиуса 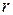с центром в начале координат, второе – область, отделенную от начала координат двумя ветвями гиперболы. Допустимое множество определяется заштрихованными областями в первом и третьем квадрантов (рис.1.1). Если наложить дополнительное требование неотрицательности переменных 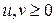, то остается только область в первом квадранте.

При некоторых видах ограничений допустимое множество может оказаться пустым. Так если в рассмотренном примере уменьшить 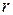, то две области могут и не пересечься.

Большинство известных методов оптимизации применимы только если допустимое множество выпукло.

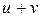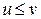Задача оптимизации не всегда имеет решение. Например, задача найти максимум функции при не имеет решения, поскольку область 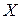не ограничена и для любого 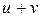можно найти другие 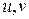дающие большие значения суммы. Однако можно выделить широкий круг задач, для которых существование оптимума гарантируется следующей теоремой.

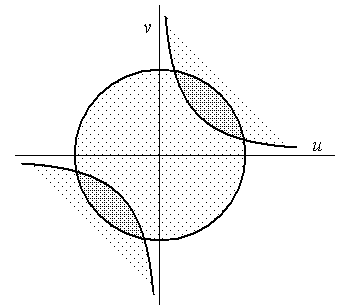
Рис. 1.1 Графическое изображение допустимого множества

Теорема Вейерштрасса. Непрерывная функция, определенная на непустом замкнутом неограниченном множестве, достигает минимума (максимума), по крайней мере, в одной из точек этого множества.

В данной теореме ключевым является требование замкнутости, поэтому оно является важным условием большинства задач оптимизации.

Для обеспечения замкнутости все ограничения на допустимое множество типа неравенств задаются как нестрогие: 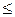или 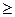. При этом знаки <,> определяют внутренние, а знаки = – граничные дочки допустимого множества.