Критерий оптимизации

На этапе постановки задачи оптимизации необходимо осуществить выбор критерия, на основе которого можно оценить характеристики системы или ее проекта, с тем, чтобы вы­явить «наилучший» проект или множество «наилучших» условий функционирования системы.

В задачах математического программирования обычно выбираются критерии экономического характера. Однако спектр возможных формулировок таких критериев весьма широк; при определении критерия могут использоваться такие экономические характеристики, как валовые капитальные затраты, издержки в единицу времени, чистая прибыль в единицу времени, доходы от инвестиций, отношение затрат к прибыли или собственный капитал на данный момент времени.

В других приложениях, критерий может основываться на некоторых технологических факторах. Например, требуется минимизировать продолжительность процесса про­изводства изделия, максимизировать темпы производства, миними­зировать количество потребляемой энергии, максимизировать ве­личину крутящего момента, максимизировать нагрузку и т. п. Независимо от того, какой критерий выбирается при оптимизации, «наилучшему» варианту всегда соответствует минимальное или мак­симальное значение показателя качества функ­ционирования системы.

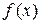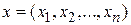Критерий оптимальности может быть представлен в виде функции параметров (целевой функции) , где - одно из допустимых решений задачи, или функционала , аргументами которого являются функции времени или координаты

.

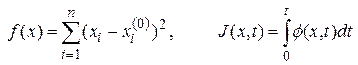Первый вариант является типичным для задач математического программирования, второй – для задач оптимального управления.

Выбор критерия оптимальности представляет собой сложную инженерную задачу, которая может быть успешно решена лишь на основе всестороннего изучения объекта управления и тех задач, которые должна выполнять система управления в целом. Величина критерия оптимальности должна отражать требования, предъявляемые к системе и к процессу управления. Обычно, к любой системе предъявляется целый ряд требований: по прибыли, издержкам и т.д., либо по точности, быстродействию, экономичности управления, надежности, стоимости, весу и т.д. Поскольку задача достижения одновременно экстремума двух и более функционалов в общем случае бессмысленна, естественно желание иметь один критерий оптимальности, который отражал бы все наиболее существенные требования к системе. Однако сформировать такой критерий трудно. Во-первых, такие требования, как надежность, стоимость, вес и др., не всегда удается выразить в математической форме. Во-вторых, объединение различных показателей в единый составной критерий имеет определенный субъективизм.

Пусть требования к системе могут быть определены в виде совокупности критериев 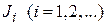, где, например, 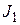характеризует точность управления, 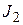– энергию, затраченную на управление, 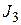– стоимость системы и т.д. Объединение этих показателей в единый обобщенный критерий может осуществляться следующими способами.

1. Составной критерий оптимальности строится в аддитивной форме

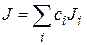. В этом случае критерий имеет наиболее простое математическое представление и это облегчает задачу оптимизации, но возникает достаточно сложная проблема определения весовых коэффициентов .

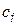2. Выделяется один основной критерий, например, 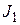, а на остальные накладываются ограничения в виде неравенств

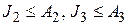и т. д.

В этом случае первичный критерий используется при оптимизации как характеристическая мера, а вторичные критерии порождают ограничения оптимизационной задачи, которые уста­навливают диапазоны изменений соответствующих показателей от минимального до максимального приемлемого значения.

Таким образом, формальное объединение требований к системе в виде обобщенного критерия оптимальности производится достаточно просто. Однако осуществить оптимизацию системы по обобщенному критерию удается не всегда. Это объясняется тем, что связь между некоторыми частными критериями и искомым оптимумом непосредственно отсутствует и проявляется лишь после реализации системы. Следовательно, получаем замкнутый круг: чтобы учесть подобные частные критерии при оптимизации системы, необходимо знать, как реализуется система, а чтобы реализовать систему, надо знать вид оптимального управления.

Особо следует указать на некоторый субъективизм при выборе обобщенного критерия оптимальности. Субъективизм проявляется при выборе частных критериев и назначении весовых коэффициентов, когда из-за недостатка знаний об объекте управления и условиях его работы приходится полагаться на интуицию и здравый смысл. Особенно это характерно для задач оптимального управления. При этом если требования к системе окажутся завышенными, их выполнение будет связано с большими трудностями или вообще окажется невозможным. Если требования низкие, то встает вопрос о целесообразности создания такой системы. Очевидно, субъективизм увеличивается с увеличением числа частных критериев, составляющих обобщенный критерий оптимальности.

Важно отметить, что независимо от содержания оптимизацион­ных методов, только один критерий может ис­пользоваться при определении оптимума, так как невозможно по­лучить решение, которое, например, одновременно обеспечивает минимум затрат, максимум надежности и минимум потребляемой энергии. Конечно, в ряде практических случаев было бы весьма желательным найти решение, которое бы являлось «наи­лучшим» с позиций нескольких различных критериев, однако это, как правило, невозможно, так как критерии противоречат друг другу.