Дерево Фейгенбаума и множество Мандельброта

Если вы когда-либо видели формулу множетсва Мандельброта z=z² + x, вы могли бы заметить схожесть между этой формулой и самой простой из формул для построения дерева Фейгенбаума x² – r. И это действительно так. Сходство существует. Но фейгенбаумово дерево растет в другую сторону. Измените формулу Фейгенбаума на x² + r и вы увидите сходство. Что касается множества Мандельброта, вам нужно смотреть вдоль горизонтальной оси, так как это единственная позиция в которой комплексная часть числа Мандельброта равна нулю. Вы увидите, что основное тело фигуры Мандельброта находится там, где функция в дереве Фейгенбаума принимает лишь одно значение. Когда происходит первое разделение линии (бифуркация) появляется новое тело на фигуре Мандельброта и т.д. Обратите также внимание на то, что когда в дереве открывается главное окно, на фигуре Мандельброта появляется дочернее тело.

Если вы когда-либо видели формулу множетсва Мандельброта z=z² + x, вы могли бы заметить схожесть между этой формулой и самой простой из формул для построения дерева Фейгенбаума x² – r. И это действительно так. Сходство существует. Но фейгенбаумово дерево растет в другую сторону. Измените формулу Фейгенбаума на x² + r и вы увидите сходство. Что касается множества Мандельброта, вам нужно смотреть вдоль горизонтальной оси, так как это единственная позиция в которой комплексная часть числа Мандельброта равна нулю. Вы увидите, что основное тело фигуры Мандельброта находится там, где функция в дереве Фейгенбаума принимает лишь одно значение. Когда происходит первое разделение линии (бифуркация) появляется новое тело на фигуре Мандельброта и т.д. Обратите также внимание на то, что когда в дереве открывается главное окно, на фигуре Мандельброта появляется дочернее тело.открывается главное окно, на фигуре Мандельброта появляется дочернее тело

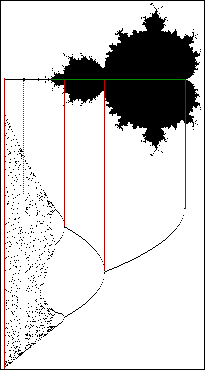
Если вы когда-либо видели формулу множетсва Мандельброта z=z² + x, вы могли бы заметить схожесть между этой формулой и самой простой из формул для построения дерева Фейгенбаума x² – r. И это действительно так. Сходство существует. Но фейгенбаумово дерево растет в другую сторону. Измените формулу Фейгенбаума на x² + r и вы увидите сходство. Что касается множества Мандельброта, вам нужно смотреть вдоль горизонтальной оси, так как это единственная позиция в которой комплексная часть числа Мандельброта равна нулю. Вы увидите, что основное тело фигуры Мандельброта находится там, где функция в дереве Фейгенбаума принимает лишь одно значение. Когда происходит первое разделение линии (бифуркация) появляется новое тело на фигуре Мандельброта и т.д. Обратите также внимание на то, что когда в дереве открывается главное окно, на фигуре Мандельброта появляется дочернее тело

Проблема Кэли
В 1879 году сэр Артур Кэли поставил задачу итерирования ком-
плексных функций. Проблема Кэли заключается в исследовании схо-
димости классического алгоритма Ньютона нахождения кубических
корней, но при условии, что вещественные числа заменяются на ком-
плексные. Для 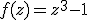нули равны кубическим корням из 1, и
итерации Ньютона принимают вид:

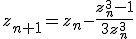
Имеются три кубических корня из единицы: , ,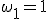
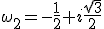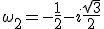
Область притяжения для корня 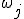есть множество .

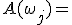
Кэли поставил задачу описания областей ; ; .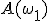
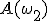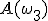Задание.
1) Для схемы итерирования

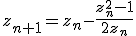
соответствующей применению метода Ньютона к 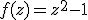, по-
кажите, что если 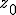лежит в правой полуплоскости, то 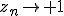при
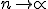, а если 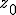лежит в левой полуплоскости, то 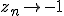при 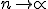. Если же 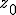лежит на мнимой оси, то процесс итерирования
не сходится.

В 1879 году Артур Кэли поставил задачу итерирования комплексных функций, которая позднее стимулировала исследования Гастона Жюлиа по проблемам теории множеств, названных теперь его именем. Проблема Кэли заключается в исследовании сходимости классического алгоритма Ньютона нахождения кубических корней, но при условии, что вещественные числа заменяются на комплексные.

Метод Ньютона для нахождения вещественного корня 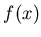(его также часто называют методом касательных) заключается в следующем. Выберем начальное приближение 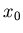, вычислим точки

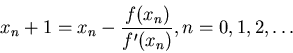
и найдем предел 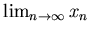. Предполагается, что 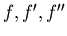существуют и непрерывны в окрестности нуля, скажем при 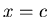. Если 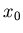находится достаточно близко к 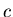и если 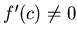, то

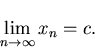
Этот метод не менее эффективен и для комплексных чисел. Это значит, что, стартовав в непосредственной близости от значения корня уравнения 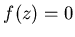, мы используя итерационный алгоритм

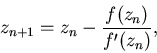
получим последовательность комплексных чисел, быстро сходящуюся к этому корню. возникает правомерный вопрос, а что будет, если начальная точка 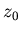выбрана в плоскости комплексных чисел не вблизи от корня, а произвольным образом?

Для 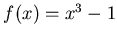нули равны кубическим корням из 1, и итерации Ньютона принимают вид:

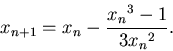
Кэли предположил исследовать поведение этих итераций для комплексных :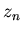

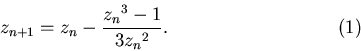
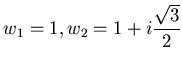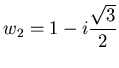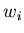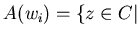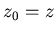Имеются три кубических корня из 1, а именно, и . Область притяжения для корня есть множество если , то .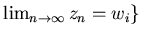

Кэли поставил задачу описания областей .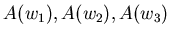

Уравнение (1) является результатом итерирования функции

Нули 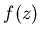являются неподвижными точками 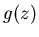, и так как

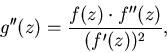
они сверхпритягивающие.

Как и в случае вещественных итераций, если начальная точка 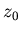находится достаточно близко к корню 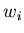, то ньютоновские итерации сходятся к этому корню. Таким образом, каждая область 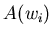содержит окрестность 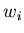. Но какую часть комплексной плоскости занимает 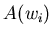и какова ее геометрия? Ответ на этот вопрос крайне нетривиален.

Рассмотрим соответствующую задачу для квадратных корней. В этом случае 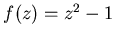и ньютоновские итерации имеют вид:

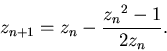
Если 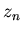лежит в правой полуплоскости, то 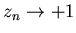при 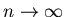, а если в левой полуплоскости, то 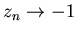при 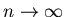. Таким образом, за исключением начальных точек 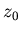, которые равноудалены от двух корней, 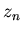сходятся к корню, ближайшему к 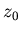. Если 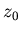лежит на мнимой оси, то в этом случае итерации не сходятся.

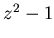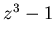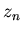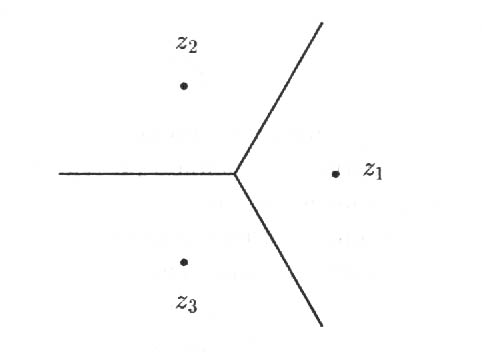
По аналогии со случаем можно предположить, что в случае итерированные значения , вычисленные по формуле (1), сходятся к кубическому корню, ближайшему к 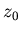, если такой ближайший корень существует. Таким образом, ответ на вопрос Кэли предположительно выглядит как пирог, разделенный на три равные части (рис.1). Как ни странно, это предположение неверно.

Теорема. Пусть 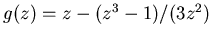- функция Ньютона для 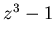. Тогда множество Жюлиа для 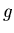имеет вид:

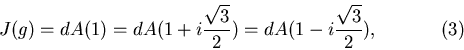
то есть 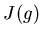является границей каждой из областей притяжения для трех притягивающих неподвижных точек: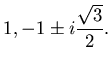

Терема говорит нам о том, что ответ на вопрос Кэли отличается от того, что изображено на рис.1. Кроме начала координат точки на границе любой области притяжения имеют малые окрестности, пересекающиеся ровно с двумя областями. Но выражение (3) говорит о том, что в произвольной окрестности каждой граничной точки любой из этих областей должны находится точки, принадлежащие всем трем областям. Правильное изображение трех бассейнов притяжения для 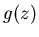было получено только с помощью компьютера (рис.).

Граница областей притяжения состоит из сильно переплетенных самоподобных фрактальных структур.

Иными словами можно задать вопрос: как закрасить плоскость тремя красками, чтобы на границе каждой цветной области существовали точки двух других цветов, которые были бы расположены произвольно близко? Ответ мы получим, раскрасив области притяжения для 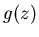разными красками.