Характеристические функции некоторых основных типов плоского потока

Исследование плоского потока методом комплексного переменного начнём с того, какие типы плоского потока соответствуют простейшим аналитическим функциям.

Исследуем течения, заданные характеристическими функциями вида

F(z) = Az и F(z) = Alnz.

I. Пусть характеристическая функция имеет вид F(z) = Az,

где z = x +iy, a A - любое комплексное или действительное число. Пусть, например, А = А₁ + iA₂.

Отделим в F (z) действительную часть от мнимой:

.

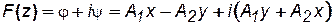Следовательно, потенциальная функция jи функция тока y выразятся следующим образом:

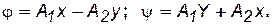(7.43)

Приравнивая полученное выражение потенциальной функции j постоянной С, найдем уравнение семейства эквипотенциальных линий:

А₁х – А₂y = С.(7.44)

Из (7.44) следует, что эквипотенциальные линии - прямые с угловым коэффициентом A₁/А₂.

Уравнение семейства линий тока найдем, приравняв выражение для y(7.43) постоянной С^*:

А₁у + А₂х = С^**.(7.45)

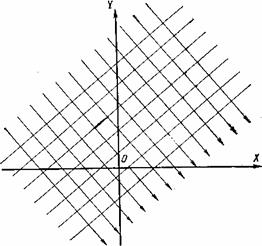
Рис. 7.21. Сетка, изображающая прямолинейно-параллельный поток в направлении, показанном стрелками.

Отсюда следует, что линии тока – прямые с угловым коэффициентом (-A₂А₁).

Таким образом, заданная характеристическая функция соответствует прямолинейно-параллельному потоку. Фильтрационное поле представлено ортогональной прямолинейной сеткой, изображенной на рис. 7.21.

Чтобы определить массовую скорость фильтрации, вычислим производную от F (z) no z. Согласно формулам (7.41) и (7.42).

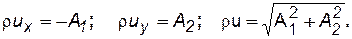
При А₁=0–поток параллелен оси 0у, а при А₂=0–параллелен оси 0х.

II. а) Пусть характеристическая функция задана в виде:

F(z) = A ln z, (7.46)

где А – некоторое действительное число.

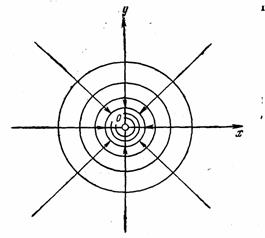
Рис. 7.22. Карта эквипотенциальных линий и линий тока

Представим комплексный аргумент z с помощью полярных коoординат так ( рис. 7.22):

z = х +i y =

=r (cos θ + i sin θ) = re^iθ, (7.47)

где г – радиус - вектор точки; θ – полярный угол.

Подставляя значение z в (7.46) и отделяя действительную часть от мнимой, получим:

F(z) = A In (re^iθ) = A In r + iAθ.

Значит

j=Alnr; y=Aθ. (7.48)

Приравнивая эти значения jи y постоянным, найдем уравнения эквипотенциальных линий и линий тока в следующем виде:

· для эквипотенциальных линий – ν=const (7.49)

· для линии тока – θ = const. (7.50)

Очевидно, эквипотенциальные линии будут концентрическими окружностями с центром в начале координат (рис. 7.22). Линии тока – прямые, проходящие через начало координат.

В данном случае имеется плоскорадиальный (сходящийся или расходящийся) поток. Центр скважины (сток или источник) находится в начале координат.

Найдем массовую скорость фильтрации, для чего вычислим производную от функции F(7.46) по z:

.

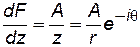Эта производная – комплексное переменное, модуль которого равен массовой скорости и представляет собой множитель перед е^-iθ.Следовательно 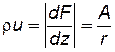, (7.51)

то есть массовая скорость фильтрации обратно пропорциональна расстоянию от скважины. (Точка г = 0 является особой точкой плоскости; здесь 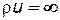и функция F (z) уже не будет аналитической). Для плоскорадиального потока имеем:

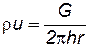, (7.52)

где G = const – массовый дебит; h– мощность пласта.

Приравнивая правые части (7.51) и (7.52), определим коэффициент А:

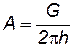. (7.53)

Подставив это значение А в формулу (7.46), получим

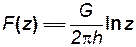, (7.54)

где положительный дебит G соответствует случаю стока (эксплуатационной скважине), а отрицательный - случаю источника (нагнетательной скважине).

Таким образом, функция (7.54) характеризует плоскорадиальное движение жидкости или газа в однородном горизонтальном пласте неограниченной протяженности. Скважина предполагается гидродинамически совершенной.

II. b) Пусть характеристическая функция имеет вид:

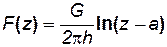, (7.55)

где а = а₁ + ia₂.

Это значит, что особая точка, в которой помещается точечный сток или точечный источник, сдвинута в направлении оси 0х на расстояние а_1., а в направлении оси 0yна расстояние a₂, и следовательно, центр поперечного сечения скважины находится не в начале координат, а в точке а = а₁ + ia₂.

Если представить комплексное переменное z-а в полярных координатах, то получим

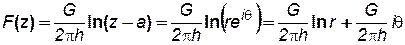, (7.56)

где r – расстояние любой точки плоскости потока не до начала координат, а до особой точки а = а₁ + ia₂, в которой помещается сток или источник; θ– полярный угол с вершиной в этой особой точке.

В соответствии с формулами (7.48) и (7.56)

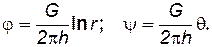(7.57)

Примечание. Потенциальная функция j и функция тока yопределяются с точностью до произвольной постоянной. В формулах (7.57), выражающих j и y, опущены произвольные постоянные, но их надо учитывать при определении дебита.

III. Пусть в основной плоскости течения имеется несколько точечных стоков и источников (несколько эксплуатационных и нагнетательных скважин).

Потенциальную функцию течения, поддерживаемого всеми стоками и источниками j, можно определить по методу суперпозиции, описанному в параграфе 7.1, как алгебраическую сумму потенциальных функций течений, поддерживаемых отдельными стоками и источниками, если бы каждый из них был единственным в пласте.

На основании первого равенства (7.57) запишем

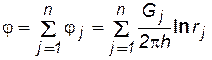, (7.58)

где G_j – массовый дебит стока или источника за номером j; r_j – расстояние любой точки плоскости потока до этого стока или источника; n – число стоков и источников.

Метод суперпозиции основан на известных свойствах уравнения Лапласа, которому подчиняется потенциал j, а именно, сумма частных решений уравнения Лапласа есть решение этого уравнения.

В то же время существование потенциальной функции j_jозначает существование наряду с ней функции тока y_j,соответствующей каждому стоку и источнику. Функция y_jудовлетворяет уравнению Лапласа; следовательно, по отношению к функции тока можно применять метод суперпозиции. Функция тока y для течения, поддерживаемого всеми стоками и источниками, определится аналогично потенциалу сложного потока:

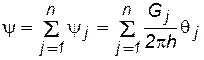. (7.59)

Характеристическая функция сложного потока, согласно формулам (7.34), (7.58, 7.59), определится уравнением:

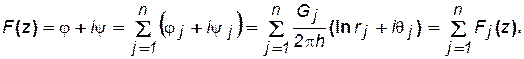(7.60)

где F_j (z) – характеристическая функция, соответствующая стоку или источнику за номером j, находящемуся в точке а_j-:

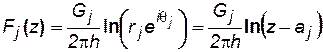. (7.61)