Решение плоских задач фильтрации методами теории функций комплексного переменного

Общие положения теории функций комплексного переменного

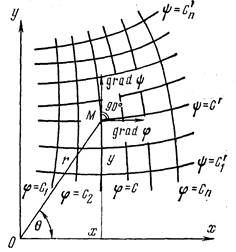
Рис. 7.19. Ортогональность изобар и линий тока

Круг задач, рассмотренных в предыдущем разделе, может быть значительно расширен, если к решениям применить аппарат теории функций комплексного переменного. При этом оказывается возможным исследовать отдельные вопросы плоского потока более полно. Рассмотрим связь между задачами плоского фильтрационного потока и теорией функций комплексного переменного.

Совместим с основной плоскостью течения плоскость комплексного переменного z = х + iy.Каждое комплексное число z изображается в этой плоскости точкой М (х, у) (рис. 7.19.). Функцией комплексного переменного z будет комплексное переменное F (z), если указан закон, позволяющий получить значение F (z) no заданному значению z.

Отделив в функции F (z) действительную часть от мнимой, можем записать

F (z) = F (х + iy) = j (х, у) + iy (х, у),(7.34)

где j(х, у) и y(х, у)-некоторые функции действительных переменных х и у; i – мнимая единица.

Задать функцию комплексного переменного - значит задать соответствие между парами чисел (х, у) и (j, y). Функция F (z) является аналитической в точке z_m,то есть имеющей производную во всех точках некоторой окрестности z_m.

В теории функций комплексного переменного имеются следующие положения:

7. Каждые две кривые, из которых одна принадлежит семейству кривых, определяемых уравнением j(х, у) = С, а другая - семейству кривых y(х, у) = С^* (С и С^* – постоянные), пересекаются под прямым углом, т. е. два семейства кривых образуют ортогональную сетку в основной плоскости течения.

2. Функции j(х, у)и y(х, у)удовлетворяют уравнению Лапласа, то есть

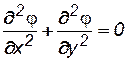; (7.35)

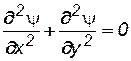. (7.36)

Положения 1 и 2 справедливы, если выполняются такие условия:

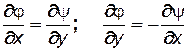. (7.37)

Условия (7.37) называются уравнениями Коши – Римана.