Характеристическая функция течения при совместном действии источника и стока

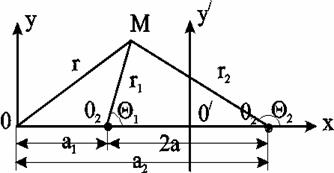
Рис. 7.23. Схема расположения источника 0₁ и стока 0₂

В разделе 7.1.6. подробно исследовалось семейство изобар в случае потока от нагнетательной скважины к эксплуатационной. О линиях тока было замечено, что они образуют семейство окружностей, ортогональных изобарам. Уточним вопрос об особенностях семейства линий тока на основе метода теории функций комплексного переменного.

Сохраняя прежние обозначения и придерживаясь рис. 7.23, получим на основании формул (7.60) и (7.61) характеристическую функцию течения от нагнетательной скважины к эксплуатационной

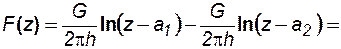. (7.62)

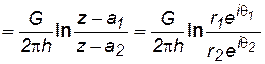
где r₁ и r₂– расстояния некоторой точки М до источника 0₁ и стока 0₂ , соответственно, θ₁ и θ₂ – соответствующие полярные углы; М – модуль массового дебита стока и источника.

Отделяя в (7.62) действительную часть от мнимой, получим

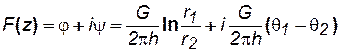, (7.63)

Отсюда:

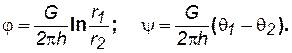, (7.64)

Из (7.64) следует, что уравнение семейства изобар запишется в виде

,

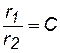где С – постоянное.

Уравнение линий тока получается из второй формулы (7.64):

θ₁-θ₂=С^*,(7.65)

где С^* – постоянное.

Рассмотрим уравнение (7.65). Выразим θ₁ и θ₂ через координаты точки М (х, у) в соответствии с рис. 7.23.

.

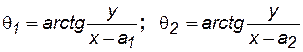Подставив значения θ₁ и θ₂ в уравнение (7.65) и учитывая, что а₂-a₁=2a, будем иметь после несложных алгебраических преобразований:

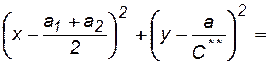(7.66)

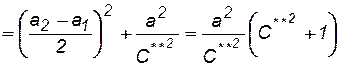
где С^** - новая постоянная.

Из (7.66) видно, что центры окружностей имеют координаты 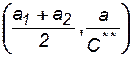. Так как абсцисса центров окружностей не зависит от С^**, то она одинакова для всех окружностей и, следовательно, все окружности расположены на прямой 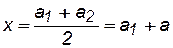, То есть на прямой, параллельной оси 0у, делящей расстояние между стоком и источником пополам. Радиус окружностей .

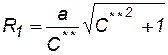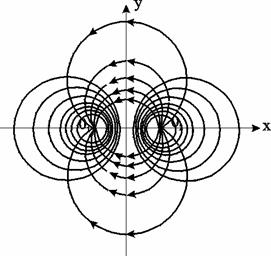
Рис. 7.24. Фильтрационное поле источника и стока

Отсюда абсциссы точек пересечения

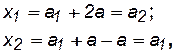
то есть линии тока проходят через сток и источник.

Таким образом, линии тока представляют собой окружности, проходящие через центры обеих скважин, и ортогональны окружностям - изобарам. Центры всех этих окружностей расположены на прямой (эквипотенциальной линии), делящей расстояние между скважинами пополам (рис. 7.24).